


Next: Limits on triple integrals
Up: Triple (Volume) Integrals
Previous: Triple (Volume) Integrals
There's absolutely no reason (other than sanity) to stop at double
integrals. Suppose we have a three dimensional object with a mass density
function given 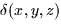 . If the volume of the object occupies a
region W of three-space, then
. If the volume of the object occupies a
region W of three-space, then
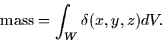
The integration is with respect to the infinitesimal volume element,
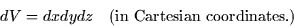
This integral (a triple integral) is an iterated integral as well.
It consists of three integrations, one in x, one in y and one in z.
If the region W is given by 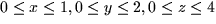 and the density function is
and the density function is 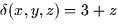 , then the mass is
, then the mass is
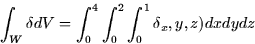
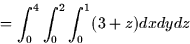
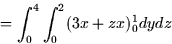
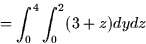
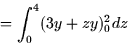
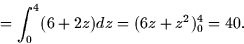
Vector Calculus
8/20/1998
![]() . If the volume of the object occupies a
region W of three-space, then
. If the volume of the object occupies a
region W of three-space, then
![]()
![]()
![]() and the density function is
and the density function is ![]() , then the mass is
, then the mass is
![]()
![]()
![]()
![]()
![]()
![]()