


Next: An example
Up: Triple (Volume) Integrals
Previous: Mass of a three
As you can probably guess, there's no reason to restrict ourselves to three
dimensional regions with constant boundaries. Any time we have an iterated
integral (and we can go beyond triple integrals) we can have the limits be
non-constant functions. There are rules, though.
- 1.
- The limits of the inner most integral can be functions of all the
other variables. Thus, if we integrate x, then y, then z, the limits
on the x integral can be functions of y and z.
- 2.
- The middle integral can have limits which depend only on the variable
in the outer integral. Continuing the example in (1), this means that the
limits on the y integral can be functions of z only.
- 3.
- The outer most integral can only have constant limits of integration.
If you want to change the order of integration, you must draw the region in
order to get the limits correct. If an integral has limits which violate
these rules, it will be impossible to draw the region. Thus, the most
general looking integral where we integrate x then y then z is of the
form
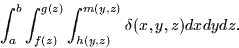



Next: An example
Up: Triple (Volume) Integrals
Previous: Mass of a three
Vector Calculus
8/20/1998
![]()