


Up: Triple (Volume) Integrals
Previous: Limits on triple integrals
Set up an iterated integral to compute the volume of a region that is
bounded by (a) the xy-plane, (b) the cone 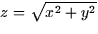 , and (c)
the cylinder x2 + y2 = 4, with a density function
, and (c)
the cylinder x2 + y2 = 4, with a density function 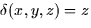 .
.
- 1.
- First, draw the region. It's the shape you'd get if you removed a
conical piece from the center of a cylinder.
(illus of region)
- 2.
- Find the limits of integration. Let's integrate in the order:
z,y,x. This gives us:
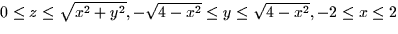 .
. - 3.
- Set up the integral and integrate:
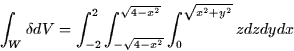
![\begin{displaymath}
= \int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \left[\frac{1}{2} z^2
\right]_0^{\sqrt{x^2+y^2}} dy dx \end{displaymath}](img83.gif)
![\begin{displaymath}
= \frac{1}{2} \int_{-2}^2 \left[x^2y +
\frac{1}{3}y^3\right]_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} dx \end{displaymath}](img85.gif)
Vector Calculus
8/20/1998
![]() , and (c)
the cylinder x2 + y2 = 4, with a density function
, and (c)
the cylinder x2 + y2 = 4, with a density function ![]() .
.
![\begin{displaymath}
= \int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \left[\frac{1}{2} z^2
\right]_0^{\sqrt{x^2+y^2}} dy dx \end{displaymath}](img83.gif)
![]()
![\begin{displaymath}
= \frac{1}{2} \int_{-2}^2 \left[x^2y +
\frac{1}{3}y^3\right]_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} dx \end{displaymath}](img85.gif)
![]()