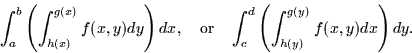The Key to getting it right

The crucial step for integrating functions over a general region is using the graph of the region to get the boundaries correct. You'll be trying to evaluate the integral $\int_R fdA$ with four boundaries, as either

$$\int_{\mbox{left}}^{\mbox{right}} \left( \int_{\mbox{bottom}... ... \left( \int_{\mbox{left}}^{\mbox{right}} f(x,y) dx \right) dy.$$

These two integrals are equivalent to breaking the region R into rectangles and then ``sweeping'' the rectangle over the region. The order of integration on the left corresponds to breaking the region up into vertical rectangles and then sweeping horizontally:

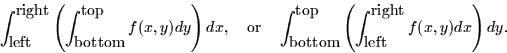
while the integral on the right corresponds sweeping horizontal rectangles vertically.

To set up the integral, first decide which order you want to integrate. We'll speak more on how to choose this in the next section. Let's say we choose to integrate in the x direction (horizontally) first. In this case, the limits on the x integral could be functions of y in order to describe the left and right boundaries. The limits on the outer integral in y must be constant, though. Otherwise, you would get a function as the result of the integral, not a number. In general,

1.

The limits on the outer integral (the last one being evaluated) must be constants.

2.

The limits on the inner integral (being evaluated first) can be constants or functions of the variable in the outer integral.

Thus, we can have double integrals of these forms:

$$\int_a^b \left(\int_{h(x)}^{g(x)} f(x,y) dy \right) dx, \qua... ... \quad \int_c^d \left( \int_{h(y)}^{g(y)} f(x,y) dx \right) dy.$$