A circular island named GUE has a population of carnivorous groo living on
it. The island has a radius of 5 km, and if we place the origin of a
coordinate system at the center of the island, the population density of
groo is given by the function ![]() . What is
the total number of groo on the island?
. What is
the total number of groo on the island?
To find this, we must integrate g(x,y) over the region, R, shown below.
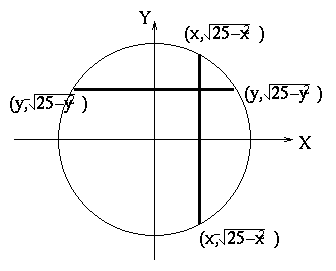
Note that the endpoints of the lines shown give the equations of the boundaries. (Recall that the equation of a circle of radius 5 centered at the origin is x2 + y2 = 25.) If we integrate bottom to top then left to right (ie. y then x) we have the boundaries:
| Boundary | Equation |
|---|---|
| left | x = -5 |
| right | x = 5 |
| bottom | |
| top |
Thus, the total population of groo is
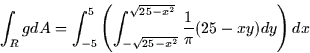
![\begin{displaymath}
= \frac{1}{\pi} \int_{-5}^5 \left[ 25y - \frac{1}{2}xy^2
\right]_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}} dx \end{displaymath}](img36.gif)
![]()