Spherical coordinates use the three variables ![]() . Here
two of the coordinates are angles, while
. Here
two of the coordinates are angles, while ![]() is the actual distance from
the origin to the point.
is the actual distance from
the origin to the point.
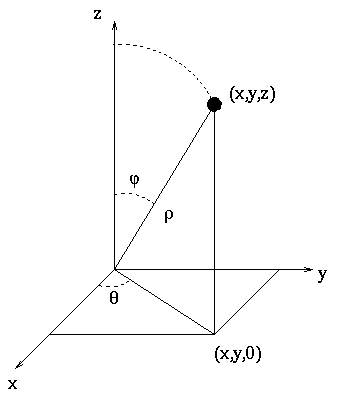
The relationship between spherical and Cartesian is a little weird:
![]()
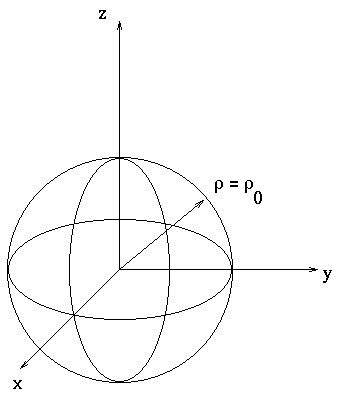
The constant coordinate surfaces are pretty intuitive. The surface ![]() describes all of the points at a distance
describes all of the points at a distance ![]() from the
origin. This is a sphere of radius
from the
origin. This is a sphere of radius ![]() .
.
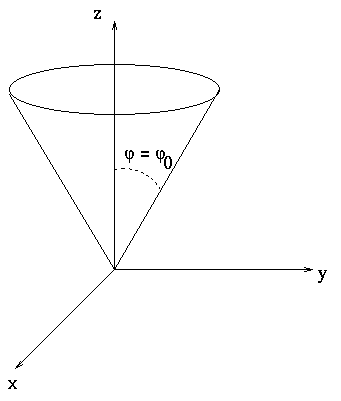
The surface ![]() is the strangest. It describes all the points
that are at an angle of
is the strangest. It describes all the points
that are at an angle of ![]() from the z-axis. This is a cone
with an
interior angle of
from the z-axis. This is a cone
with an
interior angle of ![]() with apex at the origin.
with apex at the origin.
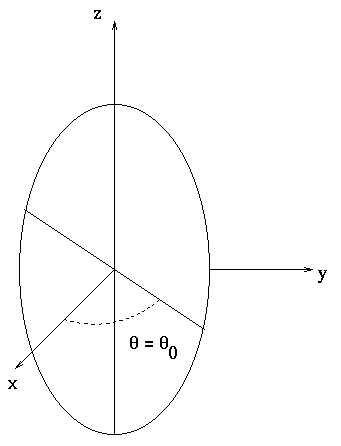
The surface ![]() describes a plane passing through the
z-axis at an angle
describes a plane passing through the
z-axis at an angle ![]() with the xaxis.
with the xaxis.