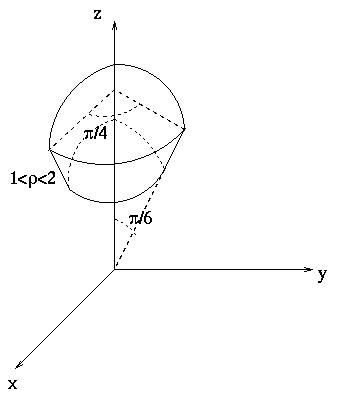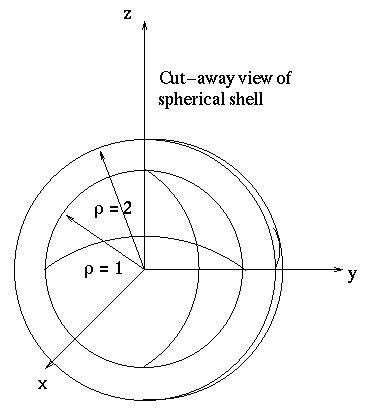
Note that the angle ![]() only ranges from 0 to
only ranges from 0 to ![]() in order to cover
the entire sphere. To see this, make a sphere of radius a by moving a
units along the z-axis, then sweeping this arc down toward the -z-axis
by rotating the line segment through
in order to cover
the entire sphere. To see this, make a sphere of radius a by moving a
units along the z-axis, then sweeping this arc down toward the -z-axis
by rotating the line segment through ![]() radians, then take the
semi-circle and rotate it through
radians, then take the
semi-circle and rotate it through ![]() radians in the
radians in the ![]() direction.
direction.