If we want to change a triple integral in xyz to a triple integral in another coordinate system, say uvw where the change of coordinates is given by
![]()
we need to compute what dV is in the new coordinate system. To find this
volume element we carry out the three dimensional version finding the area
element and use the fact that if ![]() are the
vectors along three edges of a parallelepiped, then the volume is
are the
vectors along three edges of a parallelepiped, then the volume is ![]() . This will eventually lead us to a three
dimensional version of the Jacobian:
. This will eventually lead us to a three
dimensional version of the Jacobian:
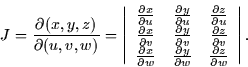
Now,
![]()
It is a very good exercise to verify that the Jacobian for cylindrical
coordinates is r and the Jacobian for spherical is ![]() .
.