


Next: The area element in
Up: Polar Coordinates
Previous: The coordinate system
Any region made up of circles, segments of circles, an annulus, or a
portion of an annulus can be easily described in polar coordinates. (An
annulus is a ring shaped region bounded by two concentric circles, one
inside the other.) Here are a few examples:
- 1.
- The upper half of a circle of radius 5, centered at the origin.
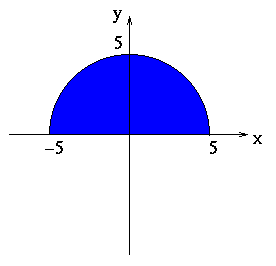
This region fills the plane in the coordinate region 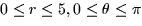 . Note that we think of this as starting at the origin
and moving along the x-axis over the range of r values, then sweeping
this line through the range of
. Note that we think of this as starting at the origin
and moving along the x-axis over the range of r values, then sweeping
this line through the range of 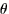 values to form the region.
values to form the region.
- 2.
- One-quarter of a circle, in the first quadrant, of radius 2,
centered on the origin.
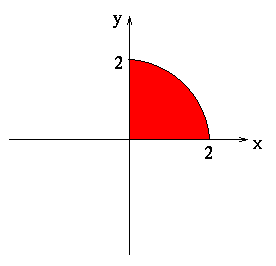
This region covers  .
.
- 3.
- The annular region between circles of radius 2 and 4, centered at the
origin, and lying in the second and third quadrants.
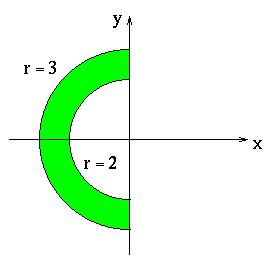
Here, the radius sweeps from 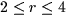 while the range of angles is
while the range of angles is
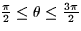 .
.
Vector Calculus
8/20/1998

![]() . Note that we think of this as starting at the origin
and moving along the x-axis over the range of r values, then sweeping
this line through the range of
. Note that we think of this as starting at the origin
and moving along the x-axis over the range of r values, then sweeping
this line through the range of ![]() values to form the region.
values to form the region.
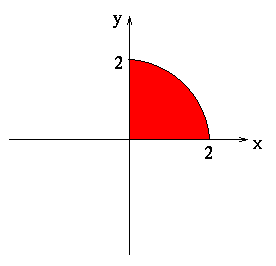
![]() .
.
![]() while the range of angles is
while the range of angles is
![]() .
.