The area element in polar coordinates

In Cartesian coordinates, a double integral is easily converted to an iterated integral:

$$\int_R fdA = \int_a^b \int_c^d f(x,y) dy dx.$$

This requires knowing that in Cartesian coordinates, dA = dy dx. What is dA in polar coordinates?

We'll follow the same path we took to get dA in Cartesian coordinates. We break up the planar region into blocks whose boundaries are described by constant functions of the variables. Then we compute the area of this region, approximating it as a very small parallelogram. Thus, we want a region bounded by $r, r + \Delta r, \theta, \theta + \Delta \theta$.

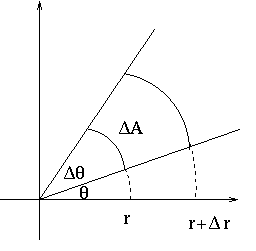
What is the area of this block of the plane?

$$\Delta A \approx \thinspace \mbox{length} \thinspace \times \thinspace \mbox{width} = (\Delta r)(r \Delta \theta).$$

Note that we have used the formula for the arc length here. In the limit as this block gets infinitesimally small, we expect to have

$$dA = r dr d\theta.$$

Thus, a double integral in polar coordinates would be

$$\int_R f dA = \int_a^b \int_c^d f(r,\theta) r dr d\theta.$$