


Next: Cylindrical Coordinates
Up: Polar Coordinates
Previous: The area element in
Compute the mass of the metal plate shown, if its density function is
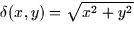 . Note that since the plate covers a
region shaped like a portion of an annulus, polar coordinates are a good
choice for integration.
. Note that since the plate covers a
region shaped like a portion of an annulus, polar coordinates are a good
choice for integration.
- 1.
- In polar coordinates, the density function becomes
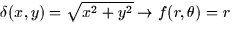 .
. - 2.
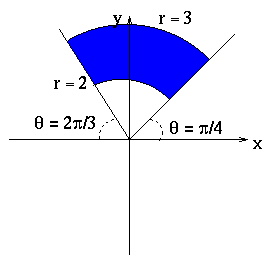
- The region of integration is
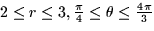 .
. - 3.
- The mass is then
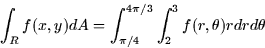
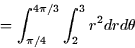
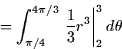
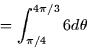
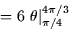
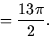
Vector Calculus
8/20/1998
![]() . Note that since the plate covers a
region shaped like a portion of an annulus, polar coordinates are a good
choice for integration.
. Note that since the plate covers a
region shaped like a portion of an annulus, polar coordinates are a good
choice for integration.

![]()
![]()
![]()
![]()
![]()
![]()