Suppose that ![]() and C is a
closed curve in the xy plane, oriented counter-clockwise as shown.
and C is a
closed curve in the xy plane, oriented counter-clockwise as shown.
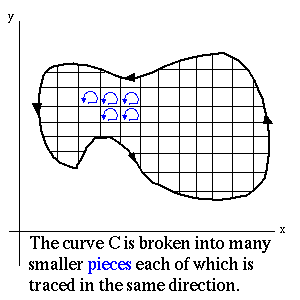
To calculate ![]() , break the area inside C
(let's call this area R) up into smaller curves,
, break the area inside C
(let's call this area R) up into smaller curves, ![]() . Make sure
that each of the
. Make sure
that each of the ![]() 's are oriented counter-clockwise as well.
Notice that we can now write the circulation of
's are oriented counter-clockwise as well.
Notice that we can now write the circulation of ![]() as
as
| (4) |
The reason this works is shown below.
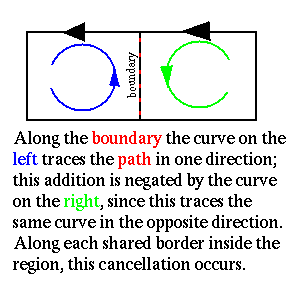
Look at the boundary of two of thess curves. Since the line integral along one of these curves is the opposite of the line integral along the other (they're following the boundary between the curves in the opposite directions) the total constribution from this inner boundary is zero. Similarly, all of the other inner boundaries cancel, leaving only the contribution from the outside boundary, which is simply C itself.
Now we look at ![]() . To calculate
this, let's assume that the dimensions of the curve are small enough that a
linear approximation to
. To calculate
this, let's assume that the dimensions of the curve are small enough that a
linear approximation to ![]() is good enough. We will treat the lower
left corner of the box-shaped curve as having coordinates (xi, yi) and
let the box have dimensions
is good enough. We will treat the lower
left corner of the box-shaped curve as having coordinates (xi, yi) and
let the box have dimensions ![]() and
and ![]() .
.