
Our linear approximation for ![]() will look like
will look like
| (5) |
where we have made the following substitutions:
![]()
![]()
![]()
Now ![]() which can be written as
which can be written as
| (6) |
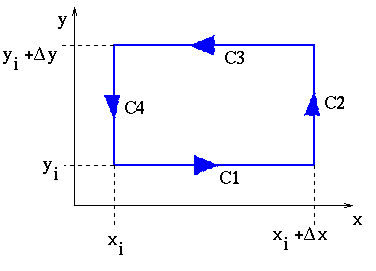
It should be easy to convince yourself that the parts of the integral involving b(x-xi)dx and p(y-yi)dy will cancel in the end, since these represent pieces of a conservative vector field, whose circulation is always zero. Likewise, a constant vector field (the pieces adx and mdy) are also conservative. The line integral now reduces to
![]()
![]()
![]()
![]()
![]()
Now we can calculate the total circulation.
![]()
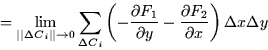
![]()