


Next: Generalizing Green's Theorem
Up: Special Case: Green's Theorem
Previous: ``The Proof''
This leads us to Green's Theorem in the Plane:
If the assumptions that
- 1.
- C is a closed curve that doesn't cross itself,
- 2.
- C encloses a region R in the xy plane,
- 3.
- C is oriented so that R is on the left as you travel in the
forward direction around C, and
- 4.
- the vector field
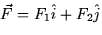 has
continuous partial derivatives as every point of R,
has
continuous partial derivatives as every point of R,
hold, then we have the result that
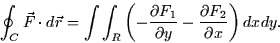
This allows us to convert between line integrals in the plane and area
integrals over the region enclosed by the curve. Note that, for a
conservative vector field this will again result in zero since the
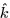 component of the curl of a conservative vector field is
component of the curl of a conservative vector field is 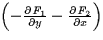 which is zero since the curl is identically the zero vector.
which is zero since the curl is identically the zero vector.
Vector Calculus
8/21/1998
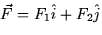 has
continuous partial derivatives as every point of R,
has
continuous partial derivatives as every point of R,