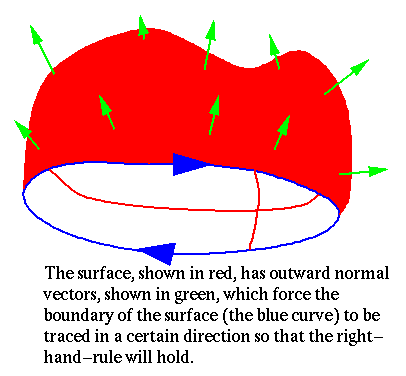
Suppose we have a closed curve C that is not necessarily in the xy plane, or even flat. Imagine that this is a ring with a film of soap spread across it. If we blow air through the ring, a soap bubble forms. Call the surface of this bubble S.

In practice, we can allow S to take any shape, so long as it has the curve C as it's boundary. This surface S is the generalized version of R from Green's Theorem. Our generalized theorem will allow us to write the circulation of a vector field around C in terms of the flux integral of the curl through any surface S which has C as its boundary.