Why This Works: The Curl as Circulation Density

Rather than treat the curl as some random thing, let's derive a more physical interpretation of the curl. We start by examining the concept of circulation density. The circulation density of a vector field $\vec{F}$ at a point P is exactly what it sounds like. We compute the circulation of the vector field around some curve C which is normal to a given vector, $\hat{n}$. We then divide by the area enclosed by the curve and shrink the whole thing down onto the point P.

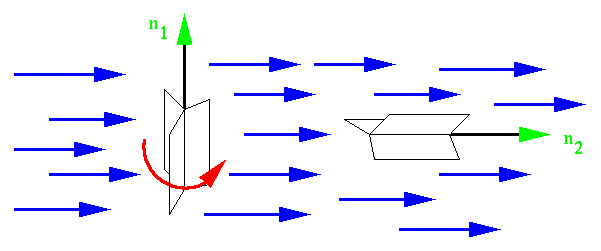
The reason we need to specify the curve as normal to some unit vector $\hat{n}$ is obvious from the example below. Circulation measures the swirl, so if we place a paddle wheel in a vector field, the paddles will rotate at a speed depending on the circulation. The higher the circulation, the faster the spin. On the left, we've placed the paddles so that they get the maximum circulation in a plane normal to the axis, $\hat{n}$. On the right, the paddle doesn't spin at all because the circulation is zero in the plane normal to $\hat{n}$.

Thus, if C is a curve around P enclosing a region of area R and having a unit normal vector $\hat{n}$, then

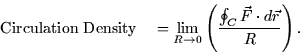$$\mbox{Circulation Density} \quad = \lim_{R \rightarrow 0} \left( \frac{\oint_C \vec{F} \cdot d\vec{r}}{R}\right).$$ (7)

A few technical details are needed here. Check the text for a reference on these.

With a little thought, we realize that the circulation density is a vector quantity. This lets us write the circulation density around a unit vector $\hat{n}$ as (letting $\hat{n} = n_1 \hat{i} + n_2 \hat{j} + n_3 \hat{k}$)

$$\left( \begin{array} {c}\mbox{circ. density}\ \mbox{around}... ...ity}\ \mbox{around} \thinspace \hat{k}\end{array} \right) n_3.$$ (8)

With a great deal of algebra, one can show that the curl of $\vec{F}$ is a vector such that

1.

it points in the direction of greatest circulation density (if it exists) and

2.

it has magnitude equal to the circulation density in that direction.