From the previous chapter on parameterization, you should remember that there are many ways to parameterize a path. Since parameterization is crucial to the concept of evaluating a line integral, what effect does this have? Let's find out.
Suppose we have a vector field ![]() where
where ![]() is the parameterization of the curve C, with parameter t. Now make a
change of parameterization. In other words, let's suppose that there is
another way to parameterize the curve using s and that
is the parameterization of the curve C, with parameter t. Now make a
change of parameterization. In other words, let's suppose that there is
another way to parameterize the curve using s and that ![]() .
Also, let's let the interval
.
Also, let's let the interval ![]() correspond to the interval
correspond to the interval
![]() . The new parameterization,
. The new parameterization, ![]() ,
so the chain rule gives us
,
so the chain rule gives us ![]() and
and
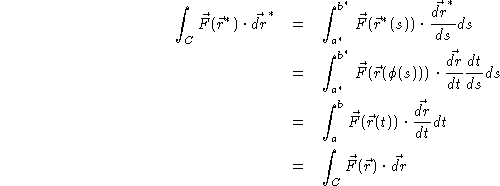
Thus, we see that changing the parameterization had no effect at all on the line integral! This property is referred to as independence of parameterization. Notice that the curve traced out in the new parameter is the same as the curve in the old parameter. The only thing that realy changed was how we traced out the curve. In general, if we were to change the path into a new curve, we would get a completely different answer.