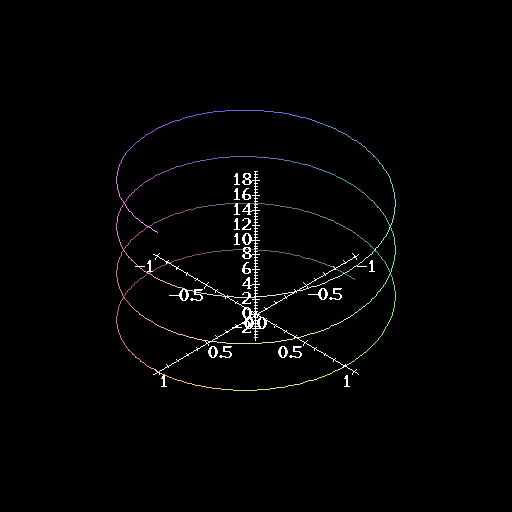
A helix looks a lot like a spring. There's an axis, along which the spring is stretched out. Let's let this be the z axis. The cross sections of the helix look like circles almost, except they they start at one value of z and wind up at a different value after coming ``full circle.''
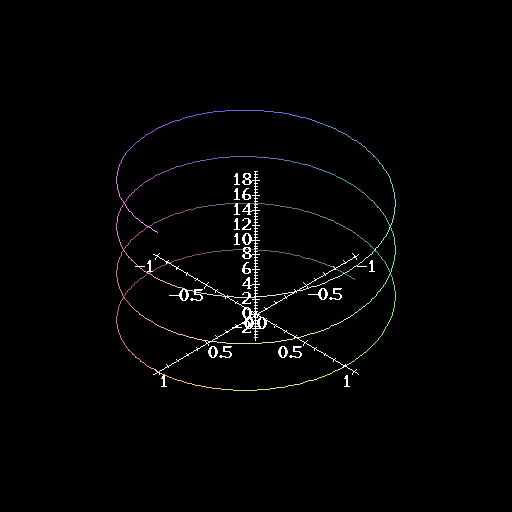
One way to generate this from a parameterization is to look at the path as being in two parts. In the xy part, we want a circle (or an ellipse):
| (23) |
In the z direction, we basically want a line:
| (24) |
Thus, the total motion can be written as the sum of these two pieces of the motion:
| (25) |