Superimposing Motions

We have already seen several examples of how to combine motions to generate new motions. The offset circle parameterization and the helix are good examples. Here's a more involved example to see how easy it can be to parameterize complicated paths.

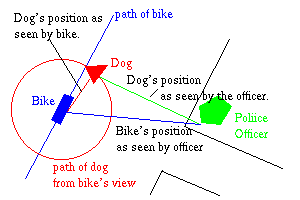
While riding a bike down the road, you notice a dog running in circles (counterclockwise) around your bike. From your point of view, the dog is making a perfect circle of radius 5 feet, centered on you. Thus, you could parameterize the dog's motion as

$$\vec{r}_{\mbox{dog}}(t) = 5 \cos t \hat{i} + 5 \sin t \hat{j}.$$ (26)

Continuing on your way, with the dog in tow, you pass a police officer on a corner. From his perspective you are traveling in a straight line through the point (2,4) (distances in feet) in the direction of the vector $\vec{v} = \hat{i} + \hat{j}$. Thus, from his perspective, your motion is along the path

$$\vec{r}_{\mbox{bike}} = (2 + t) \hat{i} + (4 + t) \hat{j}.$$ (27)

What would the police officer use as the parameterization of the motion of the dog? From his point of view, the dog makes a complicated motion that does not repeat or travel along one of the easy paths described above. However, we can turn to vector addition. By superimposing the motion of the bike with the motion of the dog as seen from the bike we get the motion as seen from the police officer:

$$\vec{r}(t) = (2 + t + 5 \cos t)\hat{i} + (4 + t + \sin t)\hat{j}.$$ (28)

In general, if $\vec{r}_{ab}$ is the parameterization of the motion of b as seen from a and $\vec{r}_{ca}$ describes the motion of a as seen from c (note the order of the subscripts gives the direction the motion is viewed) then the vector $\vec{r}_{cb} = \vec{r}_{ca} + \vec{r}_{ab}$gives the motion of b as seen by c.