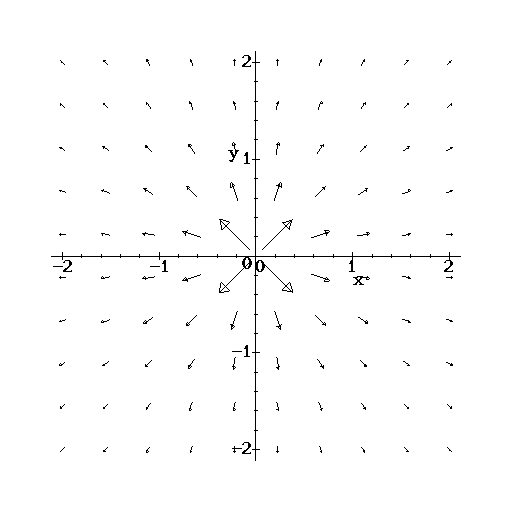
Graphically, a vector field is conservative if it has no tendency to ``swirl around.'' If it did swirl, then the value of the line integral would be path dependent. A conservative vector field has the direction of its vectors more or less evenly distributed. For example, let
| (1) |
The graphs of these vector fields are shown below. It is easy to see that
![]() is a radial vector field, and thus has no tendency to swirl. On
the other hand,
is a radial vector field, and thus has no tendency to swirl. On
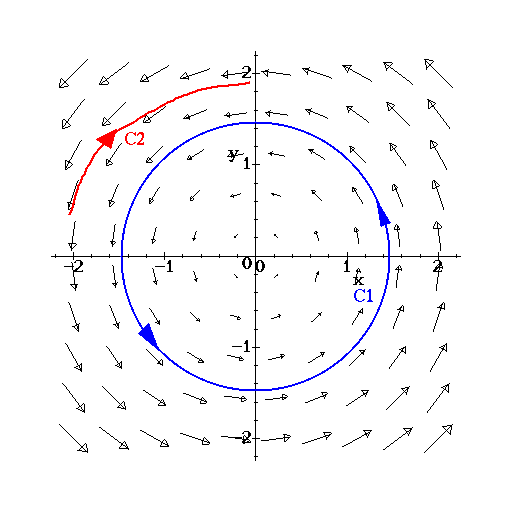
the other hand, ![]() definitely swirls around. Note that if we
compute
definitely swirls around. Note that if we
compute ![]() we get a positive value since we
are traveling along the path in the direction of the vector field. If we
compute the line integral along C2 however, we get a negative. We have
two paths between identical endpoints with different values of the line
integral, so
we get a positive value since we
are traveling along the path in the direction of the vector field. If we
compute the line integral along C2 however, we get a negative. We have
two paths between identical endpoints with different values of the line
integral, so ![]() cannot be independent of path. Thus,
cannot be independent of path. Thus, ![]() is
not conservative.
is
not conservative.