The graphical test is not very accurate. It is almost impossible to tell if a three dimensional vector field is conservative in this fashion. We can use this idea to develop an analytical approach to testing whether a vector field is conservative or not. Recall that the curl is a way to measure a vector field's tendency to swirl. Thus, to eliminate the swirling, we want
| (2) |
in order to ensure that ![]() is a conservative vector field.
is a conservative vector field.
Let's check this condition for the vector fields in the example above.
| (3) |
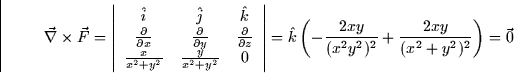 |
(4) |
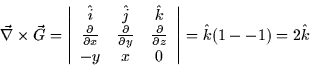 |
(5) |