The Fundamental Theorem of Calculus for Line Integrals

Suppose $\vec{F}$ is a conservative vector field. What is $\int_C \vec{F} \cdot d\vec{r}$ where C is any path from point P to point Q? Using the fact that $\vec{F}$ is conservative, we can rewrite the integral as $\int_C \mbox{grad}f \cdot d\vec{r}$. Since this integral must be independent of path, it can only depend on the values of f at points P and Q. If we divide the path up into n small segments $\Delta r_i$ and compute the integral as a Riemann sum we find

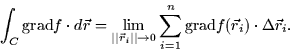$$\int_C \mbox{grad}f \cdot d\vec{r} = \lim_{\vert\vert\vec{r}... ...}\sum_{i = 1}^n \mbox{grad}f(\vec{r}_i) \cdot \Delta \vec{r}_i.$$ (14)

A little work will show that this is really just the total change in f between points P and Q. This leads us to the Fundamental Theorem of Calculus for Line Integrals:

If C is a smooth oriented curve from P to Q and f is a smooth function whose gradient is continuous on an open set containing C, then

$$\int_C \mbox{grad}f \cdot d\vec{r} = f(Q) - f(P).$$

This is the multi-variable analogue of the fundamental theorem of calculus:

$$\int_a^b f'(x)dx = f(b) - f(a).$$