Summary of Properties of Conservative Vector Fields

To summarize, if 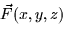$\vec{F}(x,y,z)$ is conservative, then the following are all equivalent statements.

1.

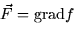$\vec{F} = \mbox{grad}f$ for some scalar potential function f.

2.

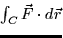$\int_C \vec{F} \cdot d\vec{r}$ is independent of path.

3.

The Fundamental Theorem of Calculus for Line Integrals (FTC4LI) holds for $\vec{F} = \mbox{grad}f$.

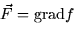4.

$\vec{\nabla} \times \vec{F} = \vec{0}$.

5.

$\vec{F}$ has no tendency to ``swirl around''.