Based on a point and a normal vector

This method relies heavily on the use of the dot product. Let's assume that we know one point that lies on the plane. Let's call this point P = (x₀, y₀, z₀). Let's also assume that we know the plane is perpendicular to the vector $\vec{n} = n_1 \hat{i} + n_2\hat{j} + n_3\hat{k}$.

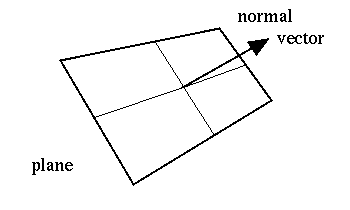
What do we know that we can use to find the equation of the plane? Notice that if we find a vector that lies in the plane, it must be perpendicular to $\vec{n}$ since the plane and the normal vector are perpendicular. Thus, the dot product of these two vectors is zero. This is an equation, if only we can find a vector in the plane.

Suppose that the point Q = (x,y,z) also lies on the plane. The displacement vector from P to Q is then a vector in the plane. The dot product of this vector, $\vec{PQ}$, and $\vec{n}$ is zero, so this will be our equation.

$$\vec{PQ} = (x - x_0)\hat{i} + (y - y_0)\hat{j} + (z - z_0)\hat{k}$$

$$\vec{n} \cdot \vec{PQ} = 0 \Rightarrow 0 = n_1 (x - x_0) + n_2 (y - y_0) + n_3 (z - z_0)$$

If we rearrange this equation, moving all of the constants to one side, we get

$$n_1 x + n_2 y + n_3 z = n_1 x_0 + n_2 y_0 + n_3 z_0, \thinsp... ...or} \thinspace z = - \frac{n_1}{n_3} x - \frac{n_2}{n_3} y + b,$$

where b = (n₁ x₀ + n₂ y₀ + n₃ z₀)/n₃. Note that in the first formula in the line above, the coefficients of x, y and z are the components of the normal vector. This is true for any plane whose formula is put into the form above. For example, the plane z = x +(1/3) y - 1 has normal vector $\vec{n} = \hat{i} + (1/3)\hat{j} - \hat{k}$. This can be seen easily after putting the equation into the form 0 = x + (1/3) y - z - 1.

As another example, what is the equation of the plane passing through the point (-1,1,0) with normal vector $\hat{i} - \hat{j} + 2 \hat{k}$? From the normal vector, we know immediately that the equation has the form

x - y + 2z = b.

By plugging in the point, we can compute b as b = (-1) + (1) + 2(0) = 0. Thus the equation for this plane is x - y + 2z = 0.

Note that there are many normal vectors to a plane. Multiplying a vector by a scalar only changes the length (and possibly orientation if the scalar is negative) of a vector. Thus, $\vec{n}$, $-\vec{n}$, and $5\vec{n}$are all normal to the same plane.