Using any three non-collinear points

Just like any two non-collinear points determine a unique line, any three non-collinear points determine a unique plane. This method requires the use of the cross product and the previous technique.

Suppose that we know the points A, B, and C all lie in a plane. Obviously, the displacement vectors $\vec{AB}$ and $\vec{AC}$ also lie in the plane. (we can actually take any two displacement vectors). Recall that the cross product of two vectors is normal to both of them. Thus, $\vec{AB} \times \vec{AC}$ is a normal vector to the plane. We can then use the idea of the previous section since we have a normal vector and a point in the plane.

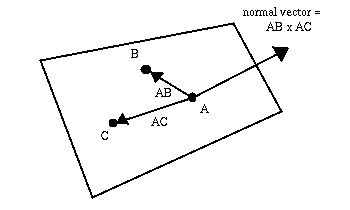
As an example, let's find the equation of the plane passing through the points A = (1,1,1), B = (-1,1,0), and C = (2,0,3). Two displacement vectors in the plane are

$$\vec{AB} = -2 \hat{i} - \hat{k} \qquad \qquad \vec{AC} = \hat{i} - \hat{j} + 2\hat{k}.$$

A vector that is normal to the plane is then

$$\vec{n} = \vec{AB} \times \vec{AC} = \left\vert \begin{array... ...1 & 2 \end{array} \right\vert = -\hat{i} + 3\hat{j} + 2\hat{k}.$$

Thus the equation of the plane has the form

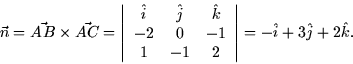
-x + 3y + 2z = b.

Plugging in one of the points, say B, we find that b = 4 so the full equation of this plane is

-x + 3y + 2z = 4.

Again note that the important thing is to find a normal vector. Since scalar multiples of a vector are still pointing in the same (or opposite) direction, they are also normal vectors. Thus, any two displacement vectors made from the three points will produce the correct equation, possibly multiplied by a constant that does not matter. The equations 3x + y - z = 2 and -6x - 2y + 2z = -4 represent the same plane since the second is simply the first equation multiplied by -2.