, 
, and 
and scalar 
:
The easy calculations above can be combined with the properties of the cross product below to calculate the cross product of two general vectors.
For any vectors, , , and and scalar :
.
.
.
Now we can construct a general formula for the cross product of two vectors:
This formula for the cross product is rather long, but notice that
the 
component of the cross product of 
and 
does
not involve the component of either vector. There is an easier way
to remember the cross product. It can be written in matrix notation as
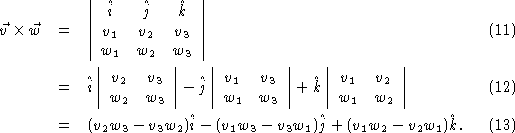
If you are familiar with matrix calculations, you should recognize this as the determinant of a three-by-three matrix. It should also be noted that, while all other vector operations are defined for vectors in any number of dimensions, the cross product is only defined for three dimensional vectors.
As an example, let's compute the cross product of the vectors 
and 
:
