and 
is written as
and has a magnitude given by
There is another way that two vectors can be multiplied. While the dot product
of two vectors produces a scalar, the cross product of two vectors is a
vector. As such, it has both magnitude and direction. The
cross product of the vectors and is written as
and has a magnitude given by
where 
is the angle between the two vectors.
The direction of the cross product is perpendicular to both of the vectors. To get the correct orientation, use the right-hand rule. Point your index finger (of your right hand) along the first vector. Then orient your hand so that your middle finger points along the second vector. Extend your thumb. It points in the direction of the cross product.
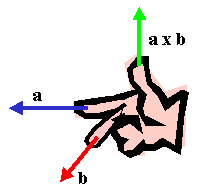
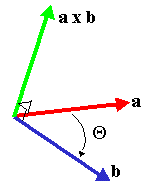
Notice that the greater the angular separation of the two vectors, the larger the cross product's magnitude.
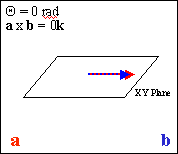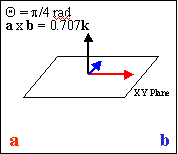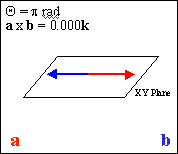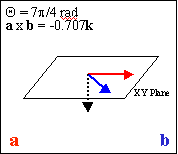
When the angle between the vectors is greater than 180 degrees, the cross product flips over to point in the opposite direction.
Now let's calculate some simple cross products.
since the angle between the vectors is
0 and 
.
since 
, and 
is perpendicular to both
vectors. Check this with the right hand rule.
since the magnitude of both vectors
is one, the angle between them is 90 and the right hand rule produces a result
in the 
direction.
Try calculating the cross product of the basis vectors in other combinations.