- (a)
- Curl
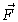 is a vector field.
is a vector field.
- (b)
- Flux of a vector field is a vector.
- (c)
- grad f is parallel to the level surface f(x,y,z) = c.
- (d)
-
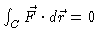 whenever C is a closed
curve.
whenever C is a closed
curve.
- (e)
-
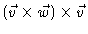 is the zero vector
for any vectors
is the zero vector
for any vectors 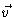 and
and  .
.
- (f)
- div (grad f) is a vector.
- (g)
-
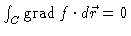 if C is a
closed curve.
if C is a
closed curve.
- (h)
- The gradient of a scalar function is a scalar.
- (i)
- A line integral is a scalar.
- (j)
- A directional derivative is a vector.
- (k)
-
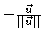 is a unit vector if
is a unit vector if
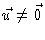 .
.
- (l)
-
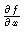 is a vector.
is a vector.
- (a)
- If
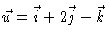 and
and
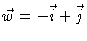 find
find
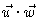 .
.
- (b)
- If f(x,y) = exy find grad f.
- (c)
- If
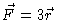 (in three dimensions) find div
(in three dimensions) find div 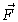 .
.
- (d)
- If
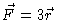 (in three dimensions) find curl
(in three dimensions) find curl 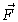 .
.
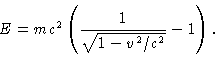
The speed, v, is non-negative and less than the speed of light, c, which is a constant.
- (a)
- Find
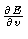 .
.
- (b)
- Explain what you would expect the sign of
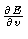 to be and why.
to be and why.
- (a)
- Use cylindrical coordinates.
- (b)
- Use spherical coordinates.
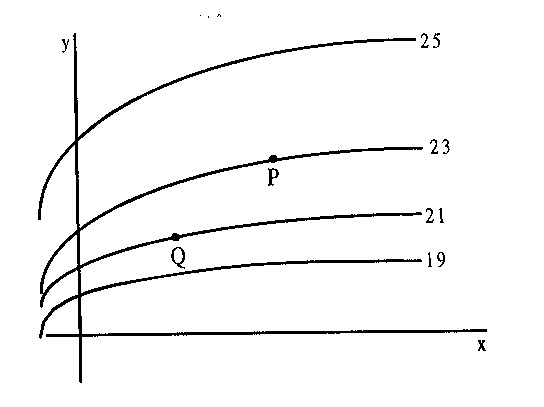
- (a)
- On the diagram above, sketch a vector at P in the direction of grad f.
- (b)
- The length of the vector grad f at P is
the length of grad f at Q? (Circle one) Give a reason.longer than shorter than the same length as - (c)
- If C is a curve going from P to Q, evaluate
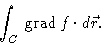
Show your reasoning.
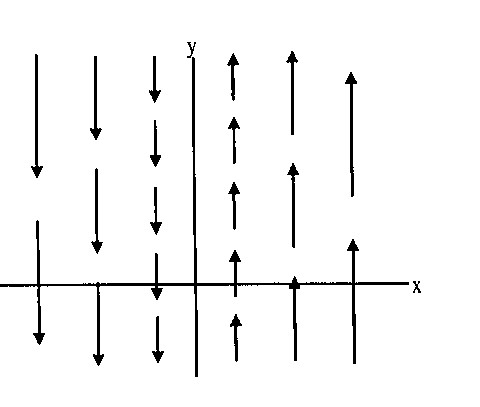
- (a)
- Do you think that
 is a conservative (that is, path
independent) vector field? Justify your answer using the
sketch.
is a conservative (that is, path
independent) vector field? Justify your answer using the
sketch.
- (b)
- Do you think that curl
 is positive,
negativeor zero? Explain.
is positive,
negativeor zero? Explain.
- (c)
- Give a possible formula for
 .
.
- (a)
- Sketch C1 and C2 on the axes below, with arrows showing
their orientation. Label your sketch clearly.
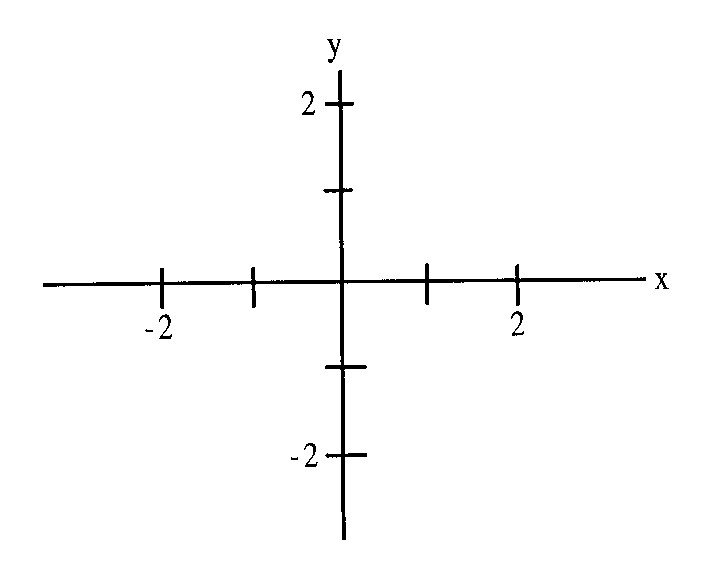
- (b)
- Suppose
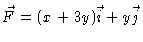 .
Calculate
.
Calculate
 ,
where C is the curve given by
C = C1 + C2. Show your work.
,
where C is the curve given by
C = C1 + C2. Show your work.
- (a)
-
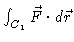 where C1 is the unit
circle in the xy-plane, orineted counterclockwise.
where C1 is the unit
circle in the xy-plane, orineted counterclockwise.
- (b)
-
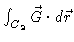 where C2 is the
y-axis from the origin to the point (0,10,0).
where C2 is the
y-axis from the origin to the point (0,10,0).
- (c)
-
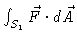 where S1 is the
cylinder
x2 + y2 = 1 with
where S1 is the
cylinder
x2 + y2 = 1 with
 ,
oriented
outward.
,
oriented
outward.
- (d)
-
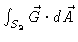 where S2 is the unit
sphere oriented outward.
where S2 is the unit
sphere oriented outward.
- (a)
- Calculate the flux of
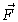 out of the unit sphere
x2 +
y2 + z2 = 1 oriented outward. Show your work.
out of the unit sphere
x2 +
y2 + z2 = 1 oriented outward. Show your work.
- (b)
- Calculate div
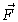 .
Show your work and simplify your
answer completely.
.
Show your work and simplify your
answer completely.
- (c)
- Use your answers to part (a) and (b) to calculate the flux of
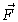 out of a box of side 10 centered at the origin with
sides parallel to the coordinate planes. (The box is also
oriented outward.) Give reasons for your answer.
out of a box of side 10 centered at the origin with
sides parallel to the coordinate planes. (The box is also
oriented outward.) Give reasons for your answer.