Fall 1998 Exam Solutions
Main menu /
Final Exams /
Fall 1998 Final
- 1.
- The answers are: T, F, F, C, F, F, T, F, T, F, T, F.
- 2.
- (a)
- 1
- (b)
-
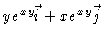
- (c)
- 9
- (d)
- 3.
-
- (a)
-
- (b)
- Since the kinetic energy of a particle increases with increasing
speed (
 )
one expects the sign of the
derivative of E with respect to v to be positive. This is
definitely true, since (1) m>0, (2) v is speed, which is the
magnitude of velocity, so v > 0, and (3) v < c implies that
1-v2/c2 > 0.
)
one expects the sign of the
derivative of E with respect to v to be positive. This is
definitely true, since (1) m>0, (2) v is speed, which is the
magnitude of velocity, so v > 0, and (3) v < c implies that
1-v2/c2 > 0.
- 4.
-
- (a)
- Taking the volume to be above the cone and below the sphere, we
find that the volume is given by (NOTE: There is a typographic error in the
following formula. The limits of integration on z should start at
r and end at SQUARE_ROOT(4-r2).)
- (b)
- In spherical coordinates, the cone is just
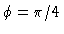 so
so
There are other possible ways to compute the volume. These are just
the simplest expressions in these two coordinate systems.
- 5.
-
- (a)
- The gradient vector should be drawn perpendicular to the
contour, from P toward the direction of increasing f, which is
toward the f=25 contour.
- (b)
- The gradient vector at P is shorter than the gradient
vector at Q because the contours at Q are closer together,
which means the function is steeper so that the rate of change of
f is larger.
- (c)
- By the Fundamental Theorem of Calculus for Line Integrals, we
have
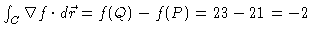 .
.
- 6.
-
- (a)
- No, the vector field shown is not conservative. If C is a
square path centered at the origin and oriented counter-clockwise,
then the circulation of
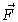 around C is clearly positive,
since the vector field always points in the same direction as the
curve, except for the two segments where it is perpendicular to
the curve. If
around C is clearly positive,
since the vector field always points in the same direction as the
curve, except for the two segments where it is perpendicular to
the curve. If 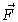 were a conservative vector field, the
circulation around any closed path would be zero.
were a conservative vector field, the
circulation around any closed path would be zero.
- (b)
- Using the same path C as in (a), we see that the circulation
of
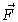 is non-zero. In fact, the right-hand rule shows that
the direction of curl
is non-zero. In fact, the right-hand rule shows that
the direction of curl 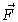 is in the
is in the 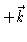 direction,
since curl
direction,
since curl
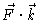 is just the circulation density
in the xy plane.
is just the circulation density
in the xy plane.
- (c)
- We know the following about
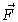 :
(1) there is no y or
z dependence in the vector field, (2) there is no
:
(1) there is no y or
z dependence in the vector field, (2) there is no 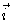 or
or
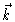 component to
component to 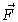 ,
(3) the magnitude of
,
(3) the magnitude of 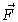 increases as you move farther from the y axis, and (4)
increases as you move farther from the y axis, and (4) 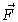 points toward
points toward 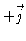 when x > 0 and
when x > 0 and 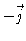 when x <
0. So,
when x <
0. So,
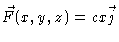 (where c is a positive
constant) is one posible formula.
(where c is a positive
constant) is one posible formula.
- 7.
-
- (a)
- The curve C1 should be a straight line from the point
(0,-1) along the y-axis to the point (0,1) and the curve
C2 should be a semicircle of radius 1 oriented counter-clockwise from
(0,1) through the point (-1,0) and down to the point
(0,-1).
- (b)
- Since the curve
C = C1 + C2 is a closed curve and is
oriented counter-clockwise, and the vector field
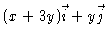 is smooth, we can use Green's theorem:
is smooth, we can use Green's theorem:
This problem can also be done by using the two parameterizations
given. However, this is much longer.
- 8.
-
- (a)
- Since the vector field
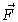 points radially outward from the
origin, it is normal to the curve C1 at all points. Thus,
points radially outward from the
origin, it is normal to the curve C1 at all points. Thus,
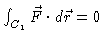 .
.
- (b)
- The vector field
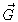 is constant and the path has a
constant tangent vector
is constant and the path has a
constant tangent vector
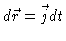 so the line
integral is just
so the line
integral is just

- (c)
- The unit normal vector for the surface is simply
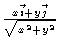 so the
so the 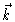 component of
component of
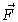 is irrelevant. Computing
is irrelevant. Computing
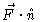 we get
we get
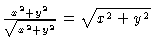 which is
just 1 on the surface of the cylinder. So
which is
just 1 on the surface of the cylinder. So
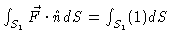 which is just (1) times
the surface area of the cylinder, which is
which is just (1) times
the surface area of the cylinder, which is
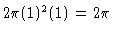 .
.
- (d)
- Since S2 is a closed surface oriented outward and the vector
field
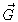 is defined on all of S2 and the volume W
inside of S2, we can use the divergence theorem. Further,
since
is defined on all of S2 and the volume W
inside of S2, we can use the divergence theorem. Further,
since 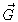 is a constant vector field, we have div
is a constant vector field, we have div
 so that
so that
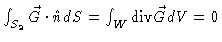 .
.
- 9.
-
- (a)
- The unit normal vector to the sphere is
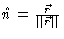 so that
so that
 since
since
 .
On the surface of the sphere,
.
On the surface of the sphere,
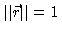 so the flux is simply
so the flux is simply
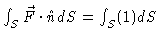 which is just the surface are of the sphere,
which is just the surface are of the sphere,
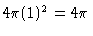 .
.
- (b)
- To calculate the divergence of
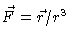 we must
first write the vector field in Cartesian coordinates. We find
we must
first write the vector field in Cartesian coordinates. We find
Then,
- (c)
- We know that we cannot directly use the divergence theorem,
since the vector field is undefined at the origin, which is inside
the region of integration. However, the vector field is radially
symmetric, so one would rather compute the flux of this vector
field through a sphere centered at the origin, rather than through
a cube. Let S be the surface of the cube and let S2 be the
surface of a sphere of radius 1, centered at the origin and
oriented outward. Let W be the volume of space inside the cube
and outside the sphere. We then have that
The first of these integrals involves a closed surface (and is oriented
outward, due to the -S2) and does not include
the origin, so that we can use the divergence theorem. Thus, using
part (b) and letting W represent the volume between the sphere and
the cube, we have
The second integral is simply the integral from part (a) which is just
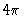 .
Thus, the divergence theorem can be used to evaluate the
integral, if one manipulates the problem correctly.
.
Thus, the divergence theorem can be used to evaluate the
integral, if one manipulates the problem correctly.
Vector Calculus
1999-05-04
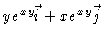
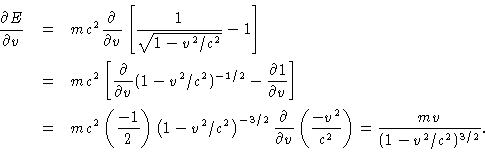
 )
one expects the sign of the
derivative of E with respect to v to be positive. This is
definitely true, since (1) m>0, (2) v is speed, which is the
magnitude of velocity, so v > 0, and (3) v < c implies that
1-v2/c2 > 0.
)
one expects the sign of the
derivative of E with respect to v to be positive. This is
definitely true, since (1) m>0, (2) v is speed, which is the
magnitude of velocity, so v > 0, and (3) v < c implies that
1-v2/c2 > 0.
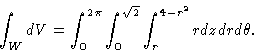
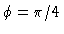 so
so
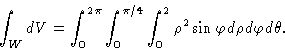
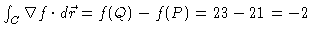 .
.
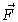 around C is clearly positive,
since the vector field always points in the same direction as the
curve, except for the two segments where it is perpendicular to
the curve. If
around C is clearly positive,
since the vector field always points in the same direction as the
curve, except for the two segments where it is perpendicular to
the curve. If 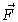 were a conservative vector field, the
circulation around any closed path would be zero.
were a conservative vector field, the
circulation around any closed path would be zero.
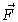 is non-zero. In fact, the right-hand rule shows that
the direction of curl
is non-zero. In fact, the right-hand rule shows that
the direction of curl 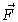 is in the
is in the 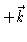 direction,
since curl
direction,
since curl
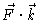 is just the circulation density
in the xy plane.
is just the circulation density
in the xy plane.
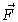 :
(1) there is no y or
z dependence in the vector field, (2) there is no
:
(1) there is no y or
z dependence in the vector field, (2) there is no 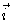 or
or
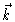 component to
component to 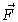 ,
(3) the magnitude of
,
(3) the magnitude of 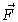 increases as you move farther from the y axis, and (4)
increases as you move farther from the y axis, and (4) 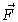 points toward
points toward 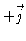 when x > 0 and
when x > 0 and 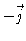 when x <
0. So,
when x <
0. So,
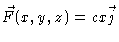 (where c is a positive
constant) is one posible formula.
(where c is a positive
constant) is one posible formula.
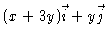 is smooth, we can use Green's theorem:
is smooth, we can use Green's theorem:

![\begin{eqnarray*}\int_C \vec{F} \cdot d\vec{r} & = & \int_{C_1} \vec{F} \cdot d\...
...\frac{\sin(2t)}{4} \right]_{\pi/2}^{3\pi/2} =
-\frac{3\pi}{2}.
\end{eqnarray*}](img19.gif)
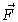 points radially outward from the
origin, it is normal to the curve C1 at all points. Thus,
points radially outward from the
origin, it is normal to the curve C1 at all points. Thus,
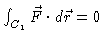 .
.
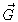 is constant and the path has a
constant tangent vector
is constant and the path has a
constant tangent vector
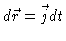 so the line
integral is just
so the line
integral is just

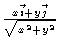 so the
so the 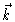 component of
component of
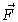 is irrelevant. Computing
is irrelevant. Computing
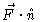 we get
we get
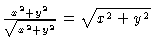 which is
just 1 on the surface of the cylinder. So
which is
just 1 on the surface of the cylinder. So
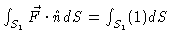 which is just (1) times
the surface area of the cylinder, which is
which is just (1) times
the surface area of the cylinder, which is
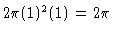 .
.
 is defined on all of S2 and the volume W
inside of S2, we can use the divergence theorem. Further,
since
is defined on all of S2 and the volume W
inside of S2, we can use the divergence theorem. Further,
since  is a constant vector field, we have div
is a constant vector field, we have div
 so that
so that
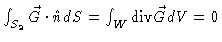 .
.
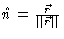 so that
so that
 since
since
 .
On the surface of the sphere,
.
On the surface of the sphere,
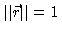 so the flux is simply
so the flux is simply
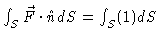 which is just the surface are of the sphere,
which is just the surface are of the sphere,
 .
.
 we must
first write the vector field in Cartesian coordinates. We find
we must
first write the vector field in Cartesian coordinates. We find
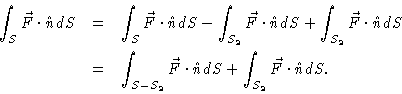
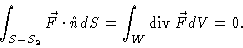
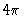 .
Thus, the divergence theorem can be used to evaluate the
integral, if one manipulates the problem correctly.
.
Thus, the divergence theorem can be used to evaluate the
integral, if one manipulates the problem correctly.