| X | |||||||||||||
| Y |
|
||||||||||||
|
|
Is f linear? Justify your answer.
PV = RT
for a certain fixed amount of gas (called a mole of gas), where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin), and R is a positive constant.- (a)
- Find
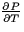 and
and 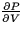 .
. - (b)
- A mole of a certain gas is at a temperature of 298 degrees Kelvin,
a pressure of 1 atmosphere, and a volume of 0.0245 m3. Calculate
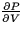 for
this gas. Give the units of your answer and explian what it means in
practical terms.
for
this gas. Give the units of your answer and explian what it means in
practical terms.
- (a)
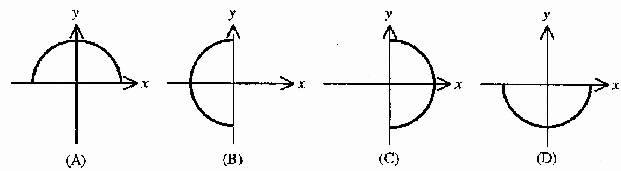
- Express
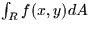 as an iterated integral, where R is the
region in the xy-plane shown below.
as an iterated integral, where R is the
region in the xy-plane shown below.
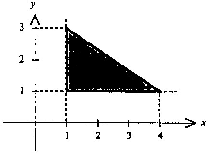
- (b)
- Evaluate
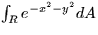 where R is the circle of
radius 2 centered at the origin.
where R is the circle of
radius 2 centered at the origin.
- (a)
- Write a brief paragraph about Stokes' Theorem. You should include
a statement of the theorem, defining any symbols used, and you should
explain in words what the theorem says.
- (b)
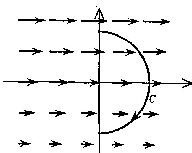
- Suppose that
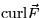 is parallel to the x-axis and
points in the direction of the positive x-axis at every point in
three-space. Suppose that C is a circle in the yz-plane, oriented
clockwise when viewed from the positive x-axis. Is the circulation of
is parallel to the x-axis and
points in the direction of the positive x-axis at every point in
three-space. Suppose that C is a circle in the yz-plane, oriented
clockwise when viewed from the positive x-axis. Is the circulation of
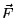 around C positive, zero, or negative? Explain your answer.
around C positive, zero, or negative? Explain your answer.
- (a)
- Find the critical points of f.
- (b)
- Classify the critical points as local maxima, minima, or saddle
points.
![]()
- (a)
- Calculate the divergence of
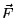 . Simplify your answer.
. Simplify your answer.
- (b)
- Use your answer in part (a) to calculate the flux of
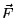 out
through the sphere of radius 1 centered at the point (0,0,2).
out
through the sphere of radius 1 centered at the point (0,0,2).
- (a)
- Find
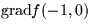 .
. - (b)
- In what direction from the point (-1,0) is f increasing most
rapidly? In what direction is the rate of change of f equal to zero?