1. No, f(x,y) is not linear because the increments of f for the
same changes in x and y is not the same in either the rows or the columns.
2. False. If ![]() and
and ![]() and perpendicular vectors, the
angle between them is
and perpendicular vectors, the
angle between them is
![]() .
The dot product is defined as
.
The dot product is defined as
3. True.
![]() so
so
![]() for all
for all ![]() .
.
4.Since ![]() and
and
![]() for
for
![]() ,
we can
make the following table:
,
we can
make the following table:
| t | x | y |
| 0 | 0 | 1 |
|
|
1 | 0 |
| 0 | -1 |
which shows the answer is c.
5. Because f(x,y) depends only on x, the contours on the
xy-plane will be straight lines up and down, parallel to the y-axis
as shown in Figure a. Constant x gives constant z.
6. The effect of the vector field on the top (y > 0) is larger and
in the direction of the orientation of the curve, than the effect on
the bottom (y<0), which is opposite to the orientation of the curve.
7. Using the curl test,
![]() .
So
.
So
![]() is not conservative.
is not conservative.
8. True, the functions are just multiples of each other.
9. Since PV = RT,
![]() so,
so,
a.
and
b. For the given conditions:
so
10.
a. The equation of the line is
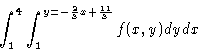
b. We know
x2 + y2 = r2 so this suggests polar coordinates:
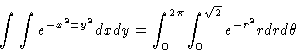
By u-substitution, with u=-r2 get
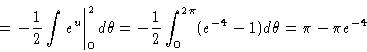
11.
a. Stokes' Theorem says that the circulation of a vector field around
the closed boundary of a capping surface is the same as the flux
through the surface. In symbols:
where:
b. In
12. To be supplied.
13.
a.
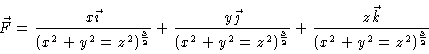
so
and
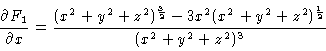
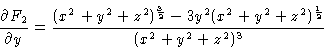
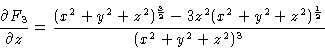
And these add to 0.
b. Since the sphere is of radius 1, and centered at (0,0,2), the
Divergence Theorem can be used, since the field ![]() is defined
everywhere within the sphere. Thus
is defined
everywhere within the sphere. Thus
14.
a.
b. The function f increases most rapidly in the direction
![]() and the rate of change is 0 along
the contour, in the directions
and the rate of change is 0 along
the contour, in the directions
![]() .
.