12.2.2 Worked Examples

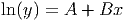
Example 12.6. Converting regression output of an exponential model
The regression output for an exponential model will be of the form

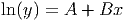
To convert this to the form ”y = …” we need to first exponentiate both sides of the equation in order to ”undo” what has been done to y. (Remember, ln(y) and exp(y) are inverse functions, so each undoes the other.) We will go step-by-step through the process.

Thus, we are left with the functional form of the equation: Y = e^A ⋅ e^BX.

To calculate (e^A) in most computer programs, use the exponentiation function, which is typically written as ”=EXP(A)”. Also note that we can use property E3 to rewrite the functional form as y = e^A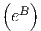x. The reason for doing this is that the base of the exponent, exp(B), tells us how much things will increase. In fact, it tells us that regardless of the current level of output in the function, if x increases by 1 unit, the output will be exp(B) times that much. (Thus, if B is a number such that exp(B) = 2, we know that increasing x by 1 unit results in the output, y, being multiplied by 2.)

Example 12.7. Converting regression output for power models
This is similar to converting an exponential model, only we need a few extra steps.

This gives us the functional form of a power model: y = 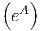x^B.

Example 12.8. Interpreting the rates of change for each model type
The examples below are taken from the data used for the introduction to this section. You can find this data in C12 Power.xls [.rda]. The response variable is the cost of the electricity produced based on the number of units of electricity produced that month (the explanatory variable.) For this data, we construct a number of different nonlinear models to try and explain the data based on the models. Note how each different model provides a different insight into the way the cost of electricity is dependent on the number of units of electricity that are produced.

1. Linear Models
   1. Equation: Y = A + Bx
   2. Interpretation: As X increases by 1, Y increases by B units
   3. Example: If Cost = 23651 + 31*Units, for each additional unit of electricity that is produced, the cost increases by $31. Thus, the constant B is measured in the units dollars per unit of electricity.
2. Exponential Models
   1. Equation: Y = Ae^BX
   2. Interpretation: As x increases by 1, y increases by a factor of (e^B - 1)
   3. Example: If we have the model ln(Cost) = 10.1592 + 0.0008 * Units, then Cost = 25828 ⋅ e^{0.0008⋅Units}, (notice: e^10.1592 = exp(10.1592) = $25,828), for each additional unit, the cost increases by (e^0.0008 - 1) ≈ 0.0008 = 0.08%. This means that if you are currently at a level of 500 units, costing $38,531, then an additional unit will increase the cost by 0.080% of $38,531, about $30.82. In this case, the units of the constant are 1/units of electricity produced; this way the product of the constant B and the variable units has no units of measurement so we can exponentiate it.
3. Logarithmic Models
   1. Equation: y = A + B * ln(x)
   2. Interpretation: As x increases by 1%, y increases approximately 0.01B
   3. Example: If Cost = -63993 + 16653 ⋅ ln(units), then if the level of production (number of units) increases 1%, then the cost increases by approximately 0.01 ⋅ 16653 = $166.53. Note that this means that the higher the production level, the greater the change required to produce the same increase in cost. At a production level of 100 units, a 1 unit increase will add about $166.53 to the cost. However, at a production level of 500, it will take a 5 unit increase in production to increase the cost by $166.53.
4. Power Models
   1. Equation: y = Ax^B
   2. Interpretation: As x increases by 1%, y increases approximately B%
   3. Example: If ln(Cost) = 7.8488 + 0.4381 ⋅ ln(Units), then Cost = 2563 ⋅ units^0.4381, since exp(7.8488) = 2563. If the production level increases 1%, then the cost will increase by about 0.4381%; that is, add a percent sign after the number B to find the percent increase. At a production level of 100 units, the cost is about $19273. If the level increases 1 unit (1%) then the cost will increase by 0.4381% of 19273 = $84. At a production level of 500, the cost is $39009, and a 1% increase in production (5 units) will increase the cost by about $171.
5. Quadratic Models
   1. Equation: y = Ax² + Bx + C
   2. Interpretation: If A is positive, then there is a minimum point at x = -B∕2A. If A is negative, then there is a maximum point at x = -B∕2A
   3. Example: Suppose we have the model: Cost = 5793 + 98.35 ⋅ Units - 0.06 ⋅ Units². Since the coefficient of units² is negative, so the model estimates there is a maximum point at a production level of -(98.35)∕2 ⋅ (-0.06) = 820units.
6. Multiplicative Models
   1. Equation from regression output: ln(y) = C + B₁ ln(x₁) + B₂ ln(X₂)
   2. Equation rewritten in standard form: Y = Ax₁^B₁x ₂^B₂. Note : exp(C) = A.
   3. Interpretation of B₁: As x₁ increases by 1%, y increases by about B₁% from its current level (holding the other explanatory variable constant)
   4. Interpretation of B₂: As x₂ increases by 1%, y increases by about B₂% from its current level (holding the other explanatory variable constant)
   5. Example: In the Cobb-Douglas model P = 0.939037L^0.7689K^0.2471 where P = Production, L = Labor, K = Capital, we see that as labor (L) increases by 1%, production increases by about 0.7689% from its current level. As capital increases by 1%, production increases by about 0.2471% from its current level. If labor is currently at 200 and capital is currently at 500, then the current level of production is 256.37, so that a 1% increase in Labor (that is, 2 more units of labor are added), then production will increase by .7689% from its current level of 256.37 which is about 1.97 units. If capital increases by 1% of 500, i.e. 5, then production will increases by 0.2471% from its current level of 256.37 (increase of about 0.63 units).

We will refer to the results of this table - the rules for interpreting the parameters in each of these different types of models - as parameter analysis. To truly understand where these guidelines come from requires a little calculus. However, you can get a pretty good understanding of why these work based simply on playing with numbers in a spreadsheet. By creating a spreadsheet that calculates values of a function, total changes in the function, total changes in the explanatory variable, and percent changes in the variables, one can easily see where the rules come from and why they are only approximate. A spreadsheet for this has been constructed and is available under C12 ParameterAnalysis.xls [.rda]. This workbook contains a worksheet for each of the basic functional models above: linear, logarithmic, exponential, power, and quadratic. Each sheet allows you to change the parameters in the model and observe how the different ways of measuring change react.