In practice, the types of interest discussed in this chapter (simple, compound, and continuously compounded) are only parts of larger schemes for determining interest. One common application of simple interest is in loan amortization. The idea is that you take out a loan for a specified amount of principal, at a particular APR, for a set period of time. This time period is broken into smaller time periods (for example, a fifteen year loan for a house might be broken into monthly payment periods) and during each period you pay back some principal and some interest. However, while the total amount of each payment is generally held constant, the amount of that payment devoted to interest and principal repayment are not. In this exploration, you will construct a spreadsheet to explore the way a loan is repaid.
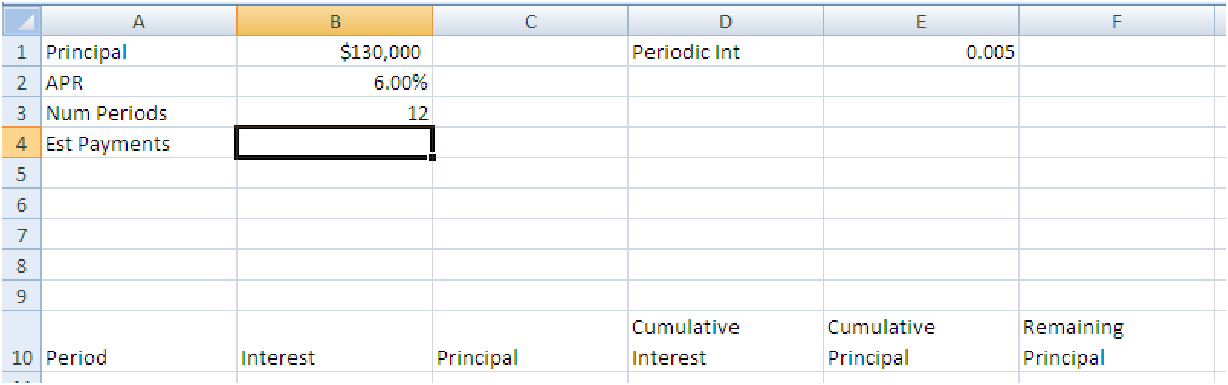
Suppose we take out a $130,000 loan for a property. If the loan is at 6% interest (APR) and we pay it back monthly over a fifteen year period (180 payments) how much will we need to pay per month? Start by entering the basic information on the loan, as shown below in cells A1:B4. In cell B4, put your guess for the amount you would expect to pay. Try to be reasonable, keeping in mind that none of the interest schemes above will actually give you the amount, since the amount of interest to be paid at any one time is determined by the remaining principal on the loan. In cell E1, enter a formula to calculate the monthly interest rate (it is the APR divided by the Number of Periods in a year). Now, set up the loan amortization table headers as shown. Under ”Period” enter the numbers 1, 2, 3, etc. up to 180 at 12 monthly periods per year, this will carry our loan through 15 years.
Now, the interest for a particular period is easy to compute: it’s just simple interest on the remaining principal balance. So, for the first period, all we need to do is multiply the periodic interest rate by the original loan amount. Once we have this, the amount of principal in the first payment is the total monthly payment minus the interest that period. The cumulative interest is just a place to track the running total on the interest we have paid and the cumulative principal tracks the total we have paid on the original loan amount; the remaining principal is the original loan minus the cumulative principal. Your formulas for the first period will probably be slightly different than the formulas for the other periods, but once you have the formulas entered, you can copy them down the table. Since the goal is to pay off the loan in 15 years (180 monthly payments) try changing the ”Est Pay” amount until you find a monthly payment that leads to a balance of zero remaining principal in period 180 (cell F190).
Once you have played with this a little, you can use ”Goal Seek” (in Excel) or uniroot in R to compute the actual monthly payment required to pay the loan off by a certain period of time. Try constructing a table listing different monthly payments based on changing one of the loan parameters (like the interest rate). Pay particular attention to the cumulative interest paid on the loan.
N.B.: There is a way to compute, just from the loan information, the monthly payment required. This formula, however, requires a lot of computational work, and we can get the same information by playing with it in our spreadsheet. Details of the formula will be discussed in the Symbolic Manipulation supplement for those interested. There are also automatic formulas in most software for computing loan amortizations. If you are interested, look up the functions PMT, IPMT and PPMT.