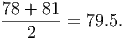
Example 4.1. Computing Mean and Median with an Odd Number of Data
Points
For this example, we want to compute the mean, median and mode of a set of test
scores:
| 55, | 60, | 67, | 70, | 78, | 81, | 84, | 88, | 90, | 95, | 99 |
The mode is the most frequently occurring observation. Since none of the test scores are repeated, there is no mode. We computed the mean of this data in example 1 and found it to be about 78.82. Computing the median of the data requires us to put the data in order (this has been done already) and identify the data point in the middle of the ordered list. There are 11 points, so we want the 6th data point (that leaves five numbers less than that observation and five greater than that observation). This makes the median 81, which is slightly higher than the mean, indicating that many students did ”above average” on the test. We call a distribution like this ”skewed to the left”, since the mean is smaller than (to the left of) the median.
| 55 | 60 | 67 | 70 | 78 | 81 | 84 | 88 | 90 | 95 | 99 |
| Lowest five | ⇑ | Highest five
| ||||||||
| observations | Median | observations | ||||||||
Example 4.2. Computing Mean and Median with an Even Number of Data
Points
Suppose that we have the same test scores as above, but a student who was absent finally comes to take the test. So now we have twelve test scores:
| 55, | 60, | 67, | 70, | 70, | 78, | 81, | 84, | 88, | 90, | 95, | 99 |
We now have 70 repeated twice, making it the most frequently occurring test score, so the mode of this set of data is 70. To compute the median, we note that with 12 data points, we need to find a score between the 6th and 7th data points. This would be
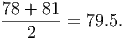
| 55 | 60 | 67 | 70 | 70 | 78 | 81 | 84 | 88 | 90 | 95 | 99 |
| Lowest five | Middle two | Highest five
| |||||||||
| observations | observations | observations | |||||||||
The mean can be computed using the same technique as above. A faster approach would be to realize that the first 11 scores (from example 1) have a mean of about 78.82. These will contribute a total of 11*78.82 = 867 to the sum of all the data . Then we add in the new data point, 70, for a total of 937, and divide by the total number of points, 12, to get the mean of the new data as approximately 78.08.
Example 4.3. Comparing Sales Performances
The data below shows the total monthly sales for each branch of Cool Toys for Tots in two different regions of the country, the north-east region and the north-central region. (See file ’C04 Tots.xls [.rda].) Which of these two regions is performing better?
| Sales NE | Sales NC |
| $95,643.20 | $668,694.31 |
| $80,000.00 | $515,539.13 |
| $543,779.27 | $313,879.39 |
| $499,883.07 | $345,156.13 |
| $173,461.46 | $245,182.96 |
| $581,738.16 | $273,000.00 |
| $189,368.10 | $135,000.00 |
| $485,344.87 | $222,973.44 |
| $122,256.49 | $161,632.85 |
| $370,026.87 | $373,742.75 |
| $140,251.25 | $171,235.07 |
| $314,737.79 | $215,000.00 |
| $134,896.35 | $276,659.53 |
| $438,995.30 | $302,689.11 |
| $211,211.90 | $244,067.77 |
| $818,405.93 | $193,000.00 |
| $141,903.82 | |
| $393,047.98 | |
| $507,595.76 | |
One way to answer this question is to compare the mean and median sales in each region. We find that the northeast region has mean sales of $325,000 and median sales of $262,974.85. The north-central region has mean sales of $300,000 and median sales of $273,000.
Based on this information, we might have a hard time deciding which region is performing better. Notice that the mean sales favor the north-east region, indicating higher sales across the region, but the median sales favor the north-central region. In fact, there are more stores in the north-central region and half of them had sales of greater than $273,000. This means that the top half of the stores in the north-central region are doing better in general than the top half of the stores in the north-east region.
Also notice that there is one store in the north-east region with sales of $818,405.93. This is much higher than the sales for the other stores in either region. This single high value is pulling the mean for the north-east region up, even though the stores in the north-central region are typically doing better.
This sensitivity to high or low scores is one of the drawbacks of the mean. This is why the Olympics (and many other sports bodies) drop the high and low scores for a competitor before computing the mean. In Chapter 3B, you’ll learn what data points like this are called and gain a powerful graphic tool for determining which data points are likely to have too much influence on the mean.