5.1.1 Definitions and Formulas

Z-scores or Standard Scores

The z-score for an observation is a dimensionless quantity that tells how many standard deviations the observation is from the mean. To compute the z-score for observation i of a variable x, we calculate:

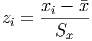
Z-scores indicate the signed distance (in standard deviations) between an observation and the mean. For example, a z-score of 0 indicates that the observation is equal to the mean, while a z-score of -1.5 indicates an observation between one and two standard deviations below the mean (because of the negative sign).

Normally Distributed Data

Statistically speaking, characteristics of a population (such as height, weight, or salary) are what are called normally distributed data. This is data that is symmetrically spread around the mean according to the normal distribution. The normal distribution itself is a product of a complicated-looking formula, but the basic idea is that the data should satisfy certain rules of thumb (see below).

Rules of Thumb

In normally distributed data, there are approximately 68% of the observations within 1 standard deviation of the mean, 95% of the observations within two standard deviations, and 99.7% within 3 standard deviations of the mean. Thus, most of the data is fairly close to the mean, with equal amounts being above and below. In terms of z-scores, the rules of thumb would say that

Z Scores	Percentage of Observations in that Range
-3 to -2	2.35%
-2 to -1	13.5%
-1 to 0	34%
0 to 1	34%
1 to 2	13.5%
2 to 3	2.35%
Total	99.7%

Thus, very few observations (0.3%) should have z-scores larger than 3 or less than -3 if the data is normally distributed. Keep in mind however, that unless you have a lot of data (several hundred observations) the rules of thumb may not be helpful for determining whether the data came from a normal distribution.