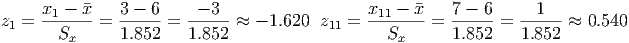
Example 5.1. Converting Observations to Z-scores
Let’s return to the data from example 2. Remember that the mean is 6 and the standard deviation
(example 3) is approximately 1.852. To calculate the z-scores, we take the observation, subtract the
mean, and divide the result by the standard deviation. A few of these are done for you. Fill in the
rest of the table on your own.
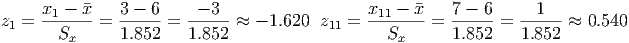
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x i | 3 | 3 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 8 | 8 | 8 | 9 |
| xi - | -3 | -3 | -2 | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 3 |
| zi | -1.6 | 0.5 | |||||||||||||
From this, we see that the smallest observations in the data (x1 and x2) are between 1 and 2 standard deviations below the mean, since the z-scores for these observations are between -1 and -2. What do you predict will happen when you add all the z-scores up? Why? Is this generally true, or special for this set of data?
Is this data from a normal distribution? That’s harder to answer. We have so few data points, that we will have a hard time matching the rules of thumb exactly. If you’ve calculated all the z-scores correctly then you should get 8 out of 15 observations with z-scores from -1 to +1. This accounts for 8/15 = 53.33% of the data, which is a little short of expectation. If this were a normal distribution, we would expect closer to 68% of 15 = 0.68 * 15 = 10.2 observations in this range. We have 15/15 = 100% of the data with z-scores between -2 and +2, which is slightly higher than the 95% expectation from the rules of thumb, but 95% of 15 = 0.95*15 = 14.25, so we are close to the right number of observations. Overall, this data does not appear to be from a normal distribution. However, to really see whether it is from a normal distribution, we need to apply some other mathematical tools. It’s entirely possible that this data really is normally distributed. We simply can’t tell with the tools we currently have, but we can make a guess that the data is not normally distributed: Specifically, there are not enough observations near the mean to make it normal.
Example 5.2. Converting from Z-scores to back to the Data
Notice that z-scores, regardless of the units of the original data, have no units themselves. This is
because units cancel out. Suppose we have data measured in dollars. Thus, the units for xi, , the
deviations from the mean, and σx are all in dollars. When we compute the z-scores, the units
vanish:
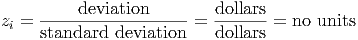
This is the power of the z-scores: they are dimensionless, so they can be used to compare data with completely different units and sizes. Everything is placed onto a standard measuring stick that is ”one standard deviation long” no matter how big the standard deviation is for a given set of data.
But suppose all we know is that a particular observation has a z-score of 1.2. What is the original data value? We know it is 1.2 standard deviations above the mean, so if we take the mean and add 1.2 standard deviations, we’ll have the original observation. So, in order to answer this question about a specific observation we need to know two things about the entire set of data: the mean and the standard deviation. So, if the data represents scores on a test in one class, and the class earned a mean score of 55 points with a standard deviation of 8 points, then a student with a standard score of 1.2 would have a real score of 55 points + 1.2(8 points) = 55 points + 12 points = 67 points. If a student in another class had a z-score of 1.5, then we know that the second student did better compared to his/her class than the first student did, because the z-score is higher. Even if the second student is in a class with a lower mean and lower standard deviation, the second student performed better relative to his/her classmates than the first student did.
On standardized tests, your score is usually reported as a type of z-score, rather than a raw score. All you really know is where your score sits relative to the mean and spread of the entire set of test-takers.
Example 5.3. Checking Rules of Thumb for the Sales Data
Does our sales data from the Cool Toys for Tots chain follow the rules of thumb for normally
distributed data? (See the new version of the data in C05 Tots.xls [.rda].) We can ask this
question from two different perspectives: by regional comparison and by comparison across the
entire chain. Let’s just look at the chain as a whole and include both the northeast and north
central regions. First, we’ll compute the z-scores for the stores in the chain in order to convert all
the data to a common ruler. For this, we’ll need the standard deviation and mean of the chain,
rather than the individual means and standard deviations for each region. The final result is shown
in the table below:
| Store | Region | Sales | Sales Z |
| 1 | NC | $668,694.31 | 2.0100 |
| 2 | NC | $515,539.13 | 1.1483 |
| 3 | NC | $313,879.39 | 0.0138 |
| 4 | NC | $345,156.13 | 0.1898 |
| 5 | NC | $245,182.96 | -0.3727 |
| 6 | NC | $273,000.00 | -0.2162 |
| 7 | NC | $135,000.00 | -0.9926 |
| 8 | NC | $222,973.44 | -0.4977 |
| 9 | NC | $161,632.85 | -0.8428 |
| 10 | NC | $373,742.75 | 0.3506 |
| 11 | NC | $171,235.07 | -0.7887 |
| 12 | NC | $215,000.00 | -0.5425 |
| 13 | NC | $276,659.53 | -0.1956 |
| 14 | NC | $302,689.11 | -0.0492 |
| 15 | NC | $244,067.77 | -0.3790 |
| 16 | NC | $193,000.00 | -0.6663 |
| 17 | NC | $141,903.82 | -0.9538 |
| 18 | NC | $393,047.98 | 0.4592 |
| 19 | NC | $507,595.76 | 1.1036 |
| 20 | NE | $95,643.20 | -1.2140 |
| 21 | NE | $80,000.00 | -1.3020 |
| 22 | NE | $543,779.27 | 1.3072 |
| 23 | NE | $499,883.07 | 1.0603 |
| 24 | NE | $173,461.46 | -0.7762 |
| 25 | NE | $581,738.16 | 1.5208 |
| 26 | NE | $189,368.10 | -0.6867 |
| 27 | NE | $485,344.87 | 0.9785 |
| 28 | NE | $122,256.49 | -1.0643 |
| 29 | NE | $370,026.87 | 0.3297 |
| 30 | NE | $140,251.25 | -0.9630 |
| 31 | NE | $314,737.79 | 0.0186 |
| 32 | NE | $134,896.35 | -0.9932 |
| 33 | NE | $438,995.30 | 0.7177 |
| 34 | NE | $211,211.90 | -0.5638 |
| 35 | NE | $818,405.93 | 2.8523 |
To check the rules of thumb, we need to determine how many stores fall into each of the breakdowns by using the z-scores.
There are 25 stores out of 35. This is 25/35 = 0.7143 = 71.43%. This value is a little higher than the rule of thumb suggests, but not by much.
There are 33 stores in this group, giving 33/35 = 0.9429 = 94.29%. This is very close to the rule of thumb.
There are 35 stores, giving 35/35 = 100% of the stores in this range. This is slightly higher than the rule of thumb suggests.
Overall, this data is fairly close to satisfying the rules of thumb for being normally distributed. There seems to be one too many observations within one standard deviation of the mean, but that is generally acceptable. (Note: 71.43% -68% = 0.0343% and 0.0343% of 35 = 1.2.) With only 35 data points, these results are very close to what one would expect from normally distributed data. Is the data symmetric? If it is, there should be roughly the same number of stores above the mean as there are below the mean.