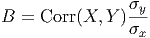This is a process for systematically determining the equation of
the best-fit line to a given set of (x,y) data. The regression equation is determined by
a process called least squares regression and results in a formula to compute the slope
and y-intercept of the line that will minimize the ”total squared error” of the line.
Based on some theoretical calculations with calculus, you can show that the slope, B,
of a regression line is given by
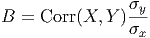
where corr(X,Y ) represents the correlation of the variable X with Y and the σ represent the
standard deviations of the X and Y variables. Once you have the slope, the y-intercept
is easy to find: A = Y - BX, where X and Y are the means of the X and Y
variables.