Example 8.1. Translating Regression Output Into an Equation
Regression output from most simple regression routines will look like the screen below. This
regression output comes from the data on backpacks in example 7 from the last chapter. The data
is in C07 Backpacks.xls [.rda]. Notice that the output is divided into three areas by headings in
bold: summary measures, ANOVA table, and regression coefficients. For right now, we are
concerned with the regression coefficients. In the next section we’ll come to understand the
summary measures (which explain how good and accurate the model is) and a little of the ANOVA
table (ANOVA stands for Analysis Of Variance; it is used for computing the summary
measures.)
| Results of simple regression for Price | |||||||
|
| |||||||
| Summary measures | |||||||
|
| Multiple R | 0.7022 | |||||
|
| R-Square | 0.4931 | |||||
|
| StErr of Est | 9.8456 | |||||
|
| |||||||
| ANOVA table | |||||||
|
| Source | df | SS | MS | F | p-value | |
|
| Explained | 1 | 2640.4857 | 2640.4857 | 27.2397 | 0.0000 | |
|
| Unexplained | 28 | 2714.1810 | 96.9350 | |||
|
| |||||||
| Regression coefficients | |||||||
|
| Lower | Upper | |||||
|
| Coefficient | Std Err | t-value | p-value | limit | limit | |
|
| Constant | -30.6751 | 13.5969 | -2.2560 | 0.0321 | -58.5272 | -2.8231 |
|
| Number of Books | 1.4553 | 0.2788 | 5.2192 | 0.0000 | 0.8842 | 2.0265 |
From this output, we can easily write down the linear equation that best estimates the price of the backpack, based on the explanatory variable ”Number of Books”. We know that ”Price” is the response variable from the first line of the regression output; it says ”Results of simple regression for Price”. The dependent variable will always be given here. To write down the regression equation, we need to know only slope and y-intercept.
The y-intercept is the ”Coefficient” next to ”Constant” in the regression coefficients portion of the output. Thus, this model has a y-intercept of -30.6751. Since the Price variable is in dollars and the y-intercept will have the same units, it probably makes sense to round this to -30.67. The slope of the regression model is the coefficient next to the explanatory variable, in this case ”Number of books”. So the slope here is 1.4553. Since number of books is typically between 10 and 60, we may want to round off to three decimal places (1.455), so that after multiplication by a number of books the result is a dollar amount.
The final regression equation is then
Price (of backpack in dollars) = -30.67 + 1.455*Number of Books.
Example 8.2. Interpreting Coefficients of a Regression Model
In the previous example, we developed a regression model from the regression output displayed
below. But what does this model mean?
The y-intercept is usually pretty clear: it’s the y-value when the x-variable is zero. So, if we were to market a backpack that couldn’t hold any books (Number of Books = 0), we could expect that people would not pay any money for it. In fact, the equation predicts that we would have to pay the customer $30.67 just to take the backpack away! After all, a backpack that doesn’t hold any books isn’t very useful. We’ll get another interpretation of this number in the next example.
To interpret the slope, we need to use some proportional reasoning. Remember that slope is rise over run. ”Run” in this case refers to the number of books the backpack will hold, while ”rise” refers to the price of the backpack. Our model has slope = rise/run = (change in y)/(change in x) = 1.455. This is marginal analysis: to determine what happens to the value of the dependent variable when x changes by 1 unit. If we design an identical backpack, that can hold one more book, then the price of the backpack will increase by $1.455. In fact, since linear models are proportional, a 2 unit increase in x will result in a 2 × $1.455 = $2.910 increase in the price.
Another way to see this is to analyze the units of the slope. Since slope is change in y over change in x, it must have the units ”y units per x unit”. Thus, our slope really means ”1.455 dollars per book”. For each additional book a backpack can hold, this model predicts a $1.455 increase in the price of the backpack.
Example 8.3. Calculating the X-intercept (Solving a linear equation)
Now, the previous examples have a y-intercept that doesn’t make much sense. After all, who would
market a backpack that you have to pay people to use? But let’s graph the equation of the model
and see if it helps. We know the y-intercept is -30.67, so the line passes through the point (0,
-30.67). It has a positive slope (1.455) so it is increasing; this means that the more books the
backpack holds, the more it is worth.

Notice that the line passes through the x-axis. Thus, it has an x-intercept. In this case, the x-intercept appears to be around Number of Books = 20, but it’s a little higher than that. Finding the x-intercept will answer the following question: What would be the least number of books the backpack would have to hold in order to be marketable? Let’s try to find the x-intercept exactly.
To do this, we take the regression equation, and we plug in everything we know is true about the x-intercept. Right now, we have a guess at its x coordinate, but that’s not good enough. We do know one thing for certain, though: it has a y-coordinate of 0. So we can plug in ”Price = 0” to our regression equation above to get
0 = -30.67 + 1.455*Number of Books.
Now, we want to use algebra to rearrange the equation to find how many books it takes to make the price zero (that’s what the above equation really means). To solve the equation, we simply ”undo” what has been done to the number of books. First, the number of books is multiplied by 1.455, then that result is added to -30.67. So, to undo it, we first subtract (-30.67) and then divide by 1.455. But if we do this to the right-hand side of the equation, we must do it to the left-hand side. Zero minus (-30.67) is just 30.67 Dividing this by 1.455, we get approximately 21.079. These steps are shown below.
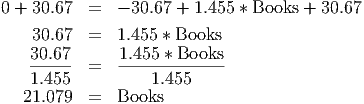
This means that unless your backpack can hold at least 22 books (the nearest whole number greater than your x intercept of 21.079, since we cannot really have a part of a book), you cannot expect anyone to buy it.