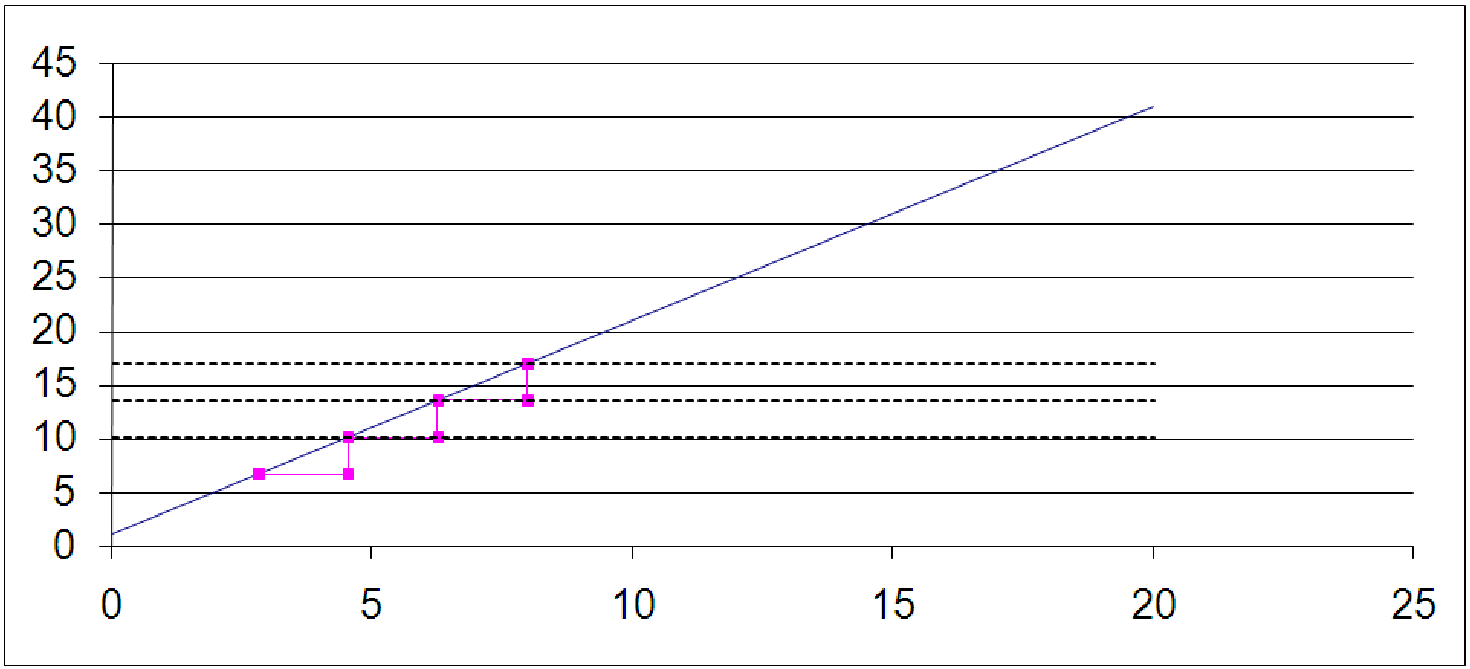
One of the main ideas of a linear function is proportionality. One way to visualize this is shown in C12 StepByStep.xls [.rda]. On the first worksheet, labeled ”linear”, you will see a straight line graphed. In addition, you will see three stair steps, three dotted lines (all horizontal) and two sliders at the top. The idea is that, in a linear function, if you walk a certain distance along the horizontal axis (the run), this forces you to climb up the function a certain amount (the rise).
If I take three steps with the same horizontal distance each, and look at the rise that this produces, I will see something interesting; I could compute this total rise from three steps by just multiplying the rise from one step by 3. This is shown by the dotted lines; each dotted line marks the rise after a certain number of steps: the first line marks your place after one step, the second line marks your place computed by doubling the first step, and the last line marks the place you would get to by tripling the first step.
Furthermore, we can play with the sliders to change both the size of the first horizontal step and the location of the starting point for the first step. Regardless of the starting point or the size of the first step, both ways of computing the place on the line result in the same amount of change.
However, this is not the case in a non-linear function. Look at the worksheet labeled ”Nonlinear”. This shows a similar set up, but with a curved graph, rather than a straight line. Here, we notice that regardless of the initial placement or the size of the first step, the two ways of computing the change are not equivalent. This is because the amount of change is level dependent in nonlinear functions.
We can summarize all of this in mathematical notation. For a linear function given by y = f(x), we find that taking n steps of size Δx results in the same answer as taking one step of size Δx and multiplying this by n. Thus, for a linear function, we find the total change in y to be
![Δy = f (x + n Δx ) - f(x ) = n [f (x + Δx ) - f(x )].
1 1 1 1](Text_Fall_2014212x.png)