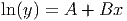
Example 12.6. Converting regression output of an exponential model
The regression output for an exponential model will be of the form
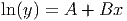
To convert this to the form ”y = …” we need to first exponentiate both sides of the equation in order to ”undo” what has been done to y. (Remember, ln(y) and exp(y) are inverse functions, so each undoes the other.) We will go step-by-step through the process.
| Algebraic Step | Explanation |
| ln(y) = A + Bx | This is the output from the regression routine, written in equation form. |
| exp(ln(y)) = exp(A + Bx) | Exp(x) is the inverse of ln(x) and if we do something to one side of an equation, we must do it to both sides of the equation. |
| y = exp(A + Bx) | Using the property that logarithms and exponentials are inverses, we know this is true. |
| y = exp(A) ⋅ exp(Bx) | Property E2. |
Thus, we are left with the functional form of the equation: Y = eA ⋅ eBX.
To calculate (eA) in most computer programs, use the exponentiation function, which is
typically written as ”=EXP(A)”. Also note that we can use property E3 to rewrite the functional
form as y = eA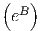 x. The reason for doing this is that the base of the exponent, exp(B), tells us
how much things will increase. In fact, it tells us that regardless of the current level of output in
the function, if x increases by 1 unit, the output will be exp(B) times that much. (Thus, if B is a
number such that exp(B) = 2, we know that increasing x by 1 unit results in the output, y, being
multiplied by 2.)
x. The reason for doing this is that the base of the exponent, exp(B), tells us
how much things will increase. In fact, it tells us that regardless of the current level of output in
the function, if x increases by 1 unit, the output will be exp(B) times that much. (Thus, if B is a
number such that exp(B) = 2, we know that increasing x by 1 unit results in the output, y, being
multiplied by 2.)
Example 12.7. Converting regression output for power models
This is similar to converting an exponential model, only we need a few extra steps.
| Algebraic Step | Explanation |
| ln(y) = A + B ln(x) | This is the output from the regression routine, written in equation form. |
| exp(ln(y)) = exp(A + B ln(x)) | Exp(x) is the inverse of ln(x) and if we do something to one side of an equation, we must do it to both sides of the equation. |
| y = exp(A + B ln(x)) | Property L2 (in disguise). |
| y = exp(A) ⋅ exp(B ln(x)) | Property E2. |
| y = exp(A) ⋅ exp(ln(xB)) | Property L5. |
| y = exp(A) ⋅ xB | Property L2 (in disguise). |
This gives us the functional form of a power model: y = 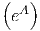 xB.
xB.
Example 12.8. Interpreting the rates of change for each model type
The examples below are taken from the data used for the introduction to this section. You can find
this data in C12 Power.xls [.rda]. The response variable is the cost of the electricity produced
based on the number of units of electricity produced that month (the explanatory variable.) For
this data, we construct a number of different nonlinear models to try and explain the data
based on the models. Note how each different model provides a different insight into the
way the cost of electricity is dependent on the number of units of electricity that are
produced.
We will refer to the results of this table - the rules for interpreting the parameters in each of these different types of models - as parameter analysis. To truly understand where these guidelines come from requires a little calculus. However, you can get a pretty good understanding of why these work based simply on playing with numbers in a spreadsheet. By creating a spreadsheet that calculates values of a function, total changes in the function, total changes in the explanatory variable, and percent changes in the variables, one can easily see where the rules come from and why they are only approximate. A spreadsheet for this has been constructed and is available under C12 ParameterAnalysis.xls [.rda]. This workbook contains a worksheet for each of the basic functional models above: linear, logarithmic, exponential, power, and quadratic. Each sheet allows you to change the parameters in the model and observe how the different ways of measuring change react.