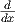 (F(x) + C) =
(F(x) + C) =
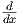 F(x) + 0 = f(x). C is called the constant of integration for the indefinite integral.
F(x) + 0 = f(x). C is called the constant of integration for the indefinite integral.
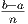 . The definite integral is denoted by ∫
abf(x)dx.
. The definite integral is denoted by ∫
abf(x)dx.
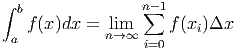
by ∑ i=0N-1f(x i)Δx, where N is a very large number. There are several different methods of numerical integration but this text uses the method of rectangles for simplicity and ease of discussion.