 x + 1. Approximate the area under the graph of y = c′(x) from x = 1 to 3 with
four rectangles.
x + 1. Approximate the area under the graph of y = c′(x) from x = 1 to 3 with
four rectangles.
Example 17.1. Approximating the Area Under a Curve
Let c′(x) =  x + 1. Approximate the area under the graph of y = c′(x) from x = 1 to 3 with
four rectangles.
x + 1. Approximate the area under the graph of y = c′(x) from x = 1 to 3 with
four rectangles.
We first find the width of each rectangle: Δx = 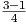 = 0.5.
= 0.5.
We next calculate the Riemann sum from 1 to 3:
(0.5[) + c (2)(0.5]) + c(2.[5)(0.5) ] [ ]
1- 1- 1- 1-
= 2(1) + 1 (0.5) + 2(1.5) + 1 (0.5) + 2(2) + 1 (0.5) + 2(2.5) + 1 (0.5 )
= [0.5 + 1](0.5) + [0.75 + 1](0.5 ) + [1 + 1](0.5) + [1.25 + 1](0.5)
= 3.75.](Text_Fall_2014367x.png)
So, the approximate area from 1 to 3 found by summing the areas of the four rectangles is 3.75. If we were to increase the number of rectangles to 16, then 64, then 1000, and then 10000, we would obtain the following results for the approximate area under the curve from 1 to 3:
| Number of Rectangles | Width of Each Rectangle | Approximation to Area |
| n = 4 | .5 | 3.75 |
| n = 16 | .125 | 3.9375 |
| n = 64 | .03125 | 3.984375 |
| n = 1000 | .002 | 3.999 |
| n = 10000 | .0002 | 3.9999 |
According to the Fundamental Theorem of Calculus (to be illustrated in example 3), the exact area under the curve from 1 to 3 is 4, which you might believe from the table, which suggests that as the number of rectangles used to estimate the area increases, the estimated area approaches the number 4. By using a very large number of rectangles, we can approximate the area under a curve quite closely. Although the calculations are staggering when computed with pencil and paper, computers can handle the computations in a fraction of a second (see Exploration 17A). The process we have described is an example of numerical integration. There are several methods other than using rectangles to compute definite integrals by numerical integration.
Example 17.2. Finding Antiderivatives for Some Basic Functions
If F is an antiderivative function of f, then F′(x) = f(x). But then F(x) + 2 is also an antiderivative function of f since the derivative of a constant, like the number 2, is zero. In general, if F(x) is an antiderivative of f, then so is F(x) + C, where C is any real number. C is called the constant of integration for F. Note: We will write the constant of integration in upper case in order to distinguish it from a function c or c(x), which we will write in lower case.
| General Rule | Examples | |
| ∫ adx = ax + C, | ∫ xdx = x + C since ∫ dx = ∫ 1 dx | |
| where a is any constant | ∫ -2 dx = -2x + C | |
| ∫ 5 dx = 5x + C | ||
∫
xn dx = 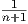 xn+1 + C xn+1 + C | ∫ xdx = 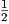 x2 + C since x = x1 x2 + C since x = x1 |
|
| where n≠ - 1 | ∫
x2 dx = 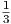 x3 + C x3 + C |
|
∫
x-3 dx = 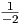 x-2 + C = - x-2 + C = -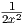 + C since -3 + 1 = 2 + C since -3 + 1 = 2 |
||
| ∫ x-1 dx = ln |x| + C | ∫ 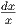 = ln |x| + C since = ln |x| + C since  = x-1 = x-1 |
|
| See note below2 | ||
| ∫ af(x) dx = a∫ f(x) dx + C | ∫
2x3 dx = 2 ∫ x3 dx = 2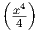 + C = + C = 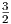 x4 + C x4 + C |
|
| where a is any constant | ∫
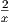 dx = 2 ∫ dx = 2 ∫
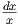 = 2 ln x + C = 2 ln x + C |
|
∫
ebx dx =  ebx + C ebx + C | ∫ e0.2x dx = 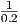 e0.2x + C = 5e0.2x + C e0.2x + C = 5e0.2x + C |
|
| ∫ 10e-0.005x dx = 10 ∫ e-0.005x dx = | ||
=  e-0.005x + C = -2000e-0.005x + C e-0.005x + C = -2000e-0.005x + C |
||
∫
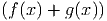 dx dx | ∫
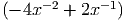 dx = dx = 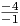 x-1 + 2 ln x + C = x-1 + 2 ln x + C = 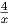 + ln x + C + ln x + C |
|
| = ∫ f(x) dx + ∫ g(x) dx | ∫
(-x2 + 4x - 2) dx = 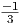 x3 + x3 + 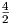 x2 - 2x + C x2 - 2x + C |
|
Example 17.3. Using the Fundamental Theorem of Calculus to Find Total and
Variable Costs from Marginal Cost
Suppose we have gathered daily marginal cost for manufacturing a particular item and found its
regression model to be c′(x) = 0.0002x2 - 0.1x + 30, where c′(x) is measured in dollars per item
and x is the number of units produced. The fixed cost of producing any number of items is
$550.
Part a. Find the total cost in producing the first 350 units per day.
Before using the Fundamental Theorem of Calculus, we need to find the antiderivative of c′(x) = 0.0002x2 - 0.1x + 30.
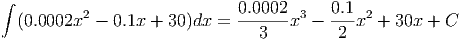
Since the fixed cost of producing zero items is $550, we know that C = 550. (Substitute x = 0 into the antiderivative and set it equal to 550; this gives C = 550). Applying the Fundamental Theorem of Calculus, we find the variable cost of producing the first 350 items:
![∫ ]350
350(0.0002x2 - 0.1x + 30)dx = 0.0002-x3 - 0.1x2 + 30x + C
0 3 2 0
[0.0002 3 0.1 2 ]
= ------(350 ) - ---(350 ) + 30(350 ) + 550 - [0 + 550]
3 2
= 0.0002(350 )3 - 0.1(350 )2 + 30(350 ) + 550 - 550
3 2
= $7233.¯33 ≈ $7233](Text_Fall_2014390x.png)
NOTE: In the definite integral, the constants of integration always cancel each other out (see 550 - 550 above). Therefore, when we compute the definite integral, we will omit the C, the constant of integration.
$7233 is the variable cost of producing the first 350 items. The total cost must include the fixed cost, $550 of producing any number of items:
Total Cost = $7233 + $550 = $7783.
Part b. What is the variable cost of producing the 151st through the 350th unit?
![]
∫ 350 2 0.0002--3 0.1 2 350
150 (0.0002x - 0.1x + 30)dx = 3 x - 2 x + 30x + C
[0.0002 0.1 150 ]
= -------(350)3 - ---(350)2 + 30(350)
[ 3 2 ]
0.0002-- 3 0.1 2
- 3 (150) - 2 (150) + 30(150)
= $3633](Text_Fall_2014391x.png)
NOTE: Since the cost of producing the 151st item begins just after having produced the 150th item, the left-hand height of the first rectangle in the Riemann sum begins at x = 150.