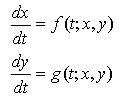
A general system of two ODEs has the form
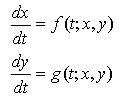
What makes a system like this linear is if the dependent variables only appear in the equation in a linear fashion. For example,
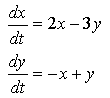
is linear, while
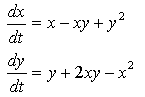
is not. The general form of a linear system of equations is given by
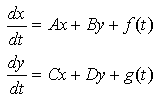
Such as system is autonomous if the independent variable, t, does not appear on the right hand side:
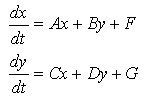
Further, if no constants appear in the equation, the system is considered homogeneous.
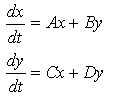
Just as with single ODEs, one feature of systems that is important to study is the existence of constant solutions. Such solutions are points in the xy-plane and are referred to as either equilibrium points or critical points for the system. If the system is solved with initial conditions that start at an equilibrium point, then the solution will remain equal to the equilibrium point for all t. To find the equilibrium points of a system, simply set all the ODEs in the system equal to zero and solve for the values of the dependent variables that make this happen.
QUESTION 1. For a general linear system of ODEs, how many equilibrium points are there and where are they located?
Written and posted by Dr. Kris H. Green, March 24, 2004