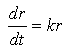
Single differential equations are useful for describing how a single quantity's rate of change varies. Solutions of such equations can be found through a variety of means - graphical analysis, analytical methods, or numerical techniques. However, most quantities in the real world are more complicated. For example, we might be interested in how the total population of rabbits in an area changes; in fact, we would probably think that the rate of change of the population of the rabbits would be proportional to the total number of rabbits, r:
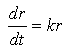
However, this would only be useful if the rabbits are isolated. More likely, there are some predators, say wolves, in the same physical region as the rabbits. If there are more wolves, more rabbits will be eaten. Without rabbits, the wolves might be likely to die off. This type of analysis led two ecologists, Lotka and Volterra, to introduce the following system of differential equations to represent the interdependence of the rabbit (r) and wolf (w) populations:
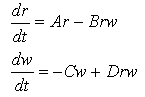
Note that in this system, all the constants (A, B, C, and D) are positive. Also note that the system of equations is autonomous, since the independent variable, t, does not appear in the system explicitly. Further, the system is nonlinear - notice that each equation has a term that involves the product of the two dependent variables, r and w. These equations are also referred to as coupled, since each equation has terms involving the both dependent variables.
The following pages will explore different aspects of systems of differential equations. We'll start with understanding linear systems and then work our way up to more complicated systems.
Written and posted by Dr. Kris H. Green, March 24, 2004