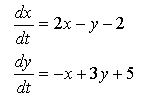
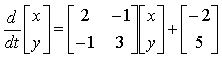
For linear systems, it is much easier to write down the system in matrix form - it's much simpler and more convenient. It's also easy to convert them from one form to another. Recall that a matrix is simply a way of keeping track of two-dimensional information in a table. A normal matrix can have any number of columns and rows. For systems of equations, each dependent variable will give us another ODE, and another row in the table. Thus, a linear system of two ODEs will result in a characteristic matrix that is 2 x 2. To write down a system of ODEs in matrix form, first write down the equations in such a way that the dependent variables appear in the same order in both equations. Also, make sure that this order is the same as the order in which the ODEs for each dependent variable are listed. Then, the characteristic matrix is simply a matrix formed by the (signed) coefficients of the terms on the right hand side of the ODEs.
For example:
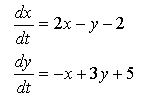 |
converts into the matrix form | 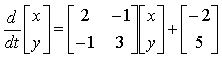 |
QUESTION 3. Try converting the system below into matrix form:
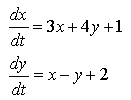
QUESTION 4. Try converting the matrix form equation below into normal form (all normal rules of matrix multiplication apply).
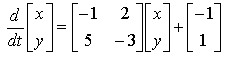
| Back to previous screen |
Written and posted by Dr. Kris H. Green, March 24, 2004