Sections

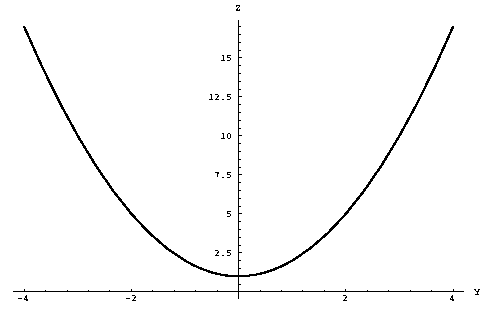
To help picture the surface that represents the function z = f(x,y) = x² + y², let's see what happens to the function if we keep one of the variables fixed and change the other. Say we keep x fixed at a value of 1. We then have z = f(1,y) = 1 + y². If we graph z as a function of y only, we get a parabola that has been shifted up one unit.

It is easy to see that if we fix x at another value, say x = c where c is some constant, then the graph of z as a function of y will still be a parabola. It will simply be shifted up by c². For each fixed value of c, the graph of z = f(c,y) is called a section of f with x fixed. The collection of all such sections is called a sectioning of f in the variable x.

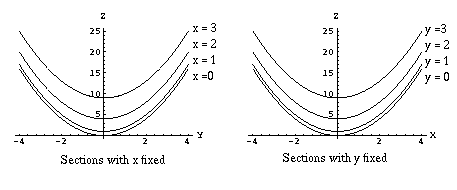
From this we try to picture the surface of the function. Imagine that the x axis comes out of the screen and move each of the sections with x = c out to the appropriate distance (c units) along the x axis. Then try to connect the sections into a single surface plot.

Click here to view an animation of this process in another window. When you are finished viewing, simply close that window to return the text here.

We can create a sectioning in either of the variables. The basic idea is to fix all but one of the variables and draw a graph as a function of the one remaining variable. This works, although is more complicated, for functions of more than two variables as well.

Here's another example. Draw x and y sectionings of the function z = g(x,y) = x² - y². To draw the sectioning in x, let x = c. We are then graphing the function z = c² - y² which are all upside down parabolas that are shifted up c² units. The sectioning in y is obtained similarly, and form right side up parabolas, that are shifted down c² units.

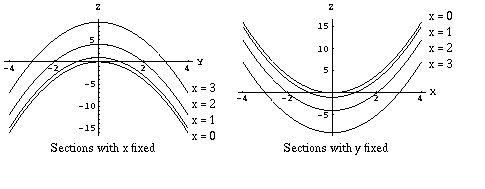
The surface that this function represents is shaped like a saddle. Can you picture it?