


Next: Flux through Surfaces defined
Up: The flux Integral
Previous: The flux Integral
We will start by considering a very special case of flux and then slowly
generalize until we have the flux integral. For now we will be considering
flowing water. We wish to find the rate at which water is flowing through
the surface S, when the velocity of the water is 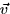 .
.
- 1.
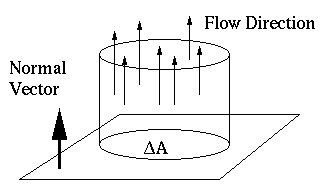
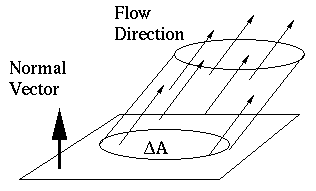
- Consider a flat surface S, which has area
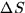 , and has been
oriented with a direction of positive flow
, and has been
oriented with a direction of positive flow 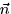 . If water is flowing
through the surface in the direction of
. If water is flowing
through the surface in the direction of 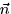 with a constant speed
with a constant speed 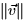 , what is the rate at which water is flowing
through S? The rate will be the total volume of water which flows past S
in a time
, what is the rate at which water is flowing
through S? The rate will be the total volume of water which flows past S
in a time 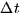 divided by
divided by 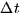 . First compute the total volume
that flows past S. The water flowing through S forms a cylinder with a
height of
. First compute the total volume
that flows past S. The water flowing through S forms a cylinder with a
height of 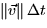 and a base with area
and a base with area 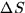 . The total volume of water will be
. The total volume of water will be
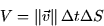
and the rate (or flux) of water through the surface will be
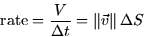
- 2.
- Next remove the condition that the direction of flow
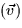 is the same as
is the same as 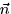 . Now we have a skewed cylinder with base S and height
. Now we have a skewed cylinder with base S and height 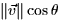 , where
, where 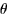 is the
angle between
is the
angle between 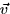 and
and 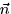 .
.(illus of skewed cylinder)
The total volume is
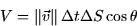
If we insist that 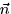 be a unit vector (I'll start using
be a unit vector (I'll start using 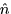 ),
then we can write the volume as
),
then we can write the volume as
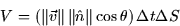
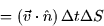
and the rate is
| 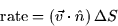 |
(1) |
- 3.
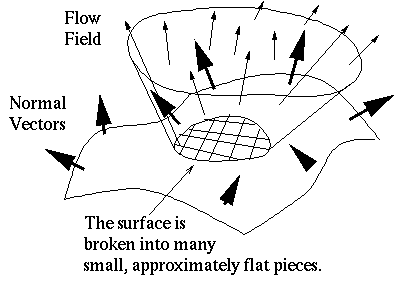
- Finally we can dispense with the assumptions that S is flat and
that
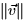 is constant. In this case we divide the
surface S into many small patches, each of which is nearly flat. Now we
can assume
is constant. In this case we divide the
surface S into many small patches, each of which is nearly flat. Now we
can assume 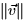 is nearly constant on each little
patch and use case 2. To get the total flux we add up the flux over all of
the small patches. Divide S into k patches
is nearly constant on each little
patch and use case 2. To get the total flux we add up the flux over all of
the small patches. Divide S into k patches 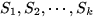 each of which has area
each of which has area 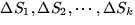 and
normal vector
and
normal vector  . Take the
velocity at the center of the jth patch (or anywhere on the patch) to
be
. Take the
velocity at the center of the jth patch (or anywhere on the patch) to
be  . Using
. Using 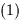 the flux through the jth patch is given by
the flux through the jth patch is given by

and the total flux is the sum over all j:
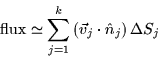
In the limit that 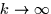 and
and 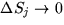 the
sum is replaced with an integral and we write
the
sum is replaced with an integral and we write
| 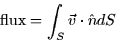 |
(2) |
Here dS is an infinitesimal piece of surface area. If we define the
vector field 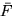 by
by
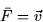
then (2) can be written as
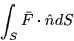
any integral of this form is called a flux integral. Sometime the quantity 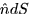 is defined to be the area vector
is defined to be the area vector 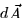 and (
and (![[*]](http://www.math.arizona.edu/~doc/latex2html/gifs/cross_ref_motif.gif) ) will be written as
) will be written as
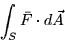
Note:

Examples:
- 1.
- Compute the flux of the vector field
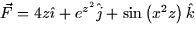 through the triangle with
vertices (0,0,0), (0,2,4), and (0,0,4) and oriented in the +x direction.
This triangle lies in the yz-plane (since x is zero for all of the
points) so the normal vector is
through the triangle with
vertices (0,0,0), (0,2,4), and (0,0,4) and oriented in the +x direction.
This triangle lies in the yz-plane (since x is zero for all of the
points) so the normal vector is 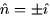 .
.
The problem says that the surface is oriented in the positive x direction
so we will use 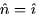 . An infinitesimal piece of area in the
yz-plane looks like dS=dydz (because the surface is flat). Therefore
. An infinitesimal piece of area in the
yz-plane looks like dS=dydz (because the surface is flat). Therefore 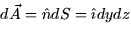 . The flux through the triangle is
. The flux through the triangle is
![\begin{displaymath}
\int_{S}\vec{F}\cdot d\vec{A} =\int_{S}\left[ 4z\hat{\imath}...
...\sin \left( x^{2}z\right) \hat{k}\right] \cdot \hat{\imath}dydz\end{displaymath}](img42.gif)
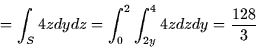
So the flux of 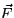 through the triangle is
through the triangle is 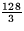 .
. - 2.
- Find the flux of
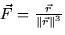 through the sphere x2+y2+z2=R2. First we notice that the
normal vector must point radially inward or outward. By convention, the
normal vector of a closed surface is taken to be outward. So
through the sphere x2+y2+z2=R2. First we notice that the
normal vector must point radially inward or outward. By convention, the
normal vector of a closed surface is taken to be outward. So 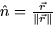 , and
, and 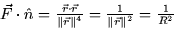 since
since 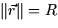 everywhere on the sphere. The flux integral is thus
everywhere on the sphere. The flux integral is thus
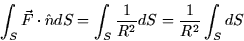
The last integral is the surface area of a sphere of radius R.
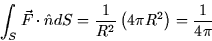



Next: Flux through Surfaces defined
Up: The flux Integral
Previous: The flux Integral
Vector Calculus
8/21/1998
![]() .
.![]()
![]()

![]()
![]()
![]()

![]()
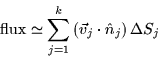
![]()
![]()
![[*]](http://www.math.arizona.edu/~doc/latex2html/gifs/cross_ref_motif.gif) ) will be written as
) will be written as
![]()
![]()


![]() . An infinitesimal piece of area in the
yz-plane looks like dS=dydz (because the surface is flat). Therefore
. An infinitesimal piece of area in the
yz-plane looks like dS=dydz (because the surface is flat). Therefore ![]() . The flux through the triangle is
. The flux through the triangle is
![]()
![]()
![]()
![]()