


Next: Flux Through Cylinders
Up: The flux Integral
Previous: Introduction
Now we need to find 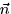 and dS. If the surface S is defined by a
function, z=g(x,y) we can obtain a nice expression for
and dS. If the surface S is defined by a
function, z=g(x,y) we can obtain a nice expression for 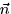 and dS.
For the normal vector to S at the point (x0,y0,g(x0,y0)) we
can use the normal vector to the tangent plane. Remember that the tangent
plane to g(x,y) at the point (x0,y0) is given by:
and dS.
For the normal vector to S at the point (x0,y0,g(x0,y0)) we
can use the normal vector to the tangent plane. Remember that the tangent
plane to g(x,y) at the point (x0,y0) is given by:
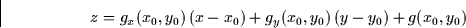
or
-gx(x0,y0)x-gy(x0,y0)y+z=c
where c=-gx(x0,y0)x0-gy(x0,y0)y0+g(x0,y0). A
normal vector to the tangent plane is
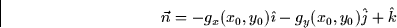
If we normalize 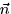 to get a unit normal vector we get
to get a unit normal vector we get
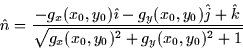
So the normal vector as a function of 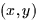 is
is
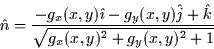
The Area of the jth patch can be obtained by finding the vectors 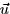 ,
, 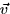 which define the edges of the patch (one parallel to the xz-plane and one parallel to the yz-plane????). The area of the patch is
given by
which define the edges of the patch (one parallel to the xz-plane and one parallel to the yz-plane????). The area of the patch is
given by 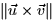 . If we employ the tangent
plane approximation of g(x,y)we can see that
. If we employ the tangent
plane approximation of g(x,y)we can see that 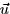 is the vector from (x0,y0,g(x0,y0)) to
is the vector from (x0,y0,g(x0,y0)) to 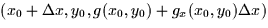 or
or
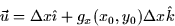
Similarly 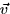 is the vector that points from (x0,y0,g(x0,y0)) to the point
is the vector that points from (x0,y0,g(x0,y0)) to the point 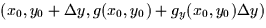 or
or
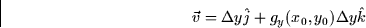
Taking the cross product of 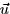 and
and 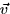 gives
gives
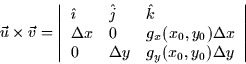
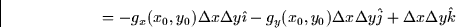
Finally, the area of the jth patch is
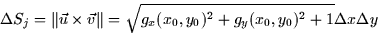
In the limit that 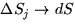 this becomes
this becomes
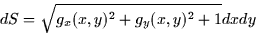
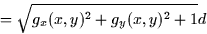
When we put these together we get
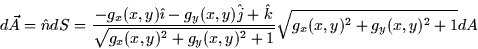
| 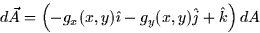 |
(3) |
So we've represented the integral over the surface in terms of an integral
over the region R in the xy-plane over which S sits.
![\begin{displaymath}
\int_{S}\vec{F}\cdot d\vec{A}=\int_{S}\vec{F}\cdot \hat{n}dS...
...x,y)\hat{\imath}-g_{y}(x,y)\hat{j}+\hat{k}\right)
\right] dA
\end{displaymath}](img71.gif)
Where R is the ''shadow'' of S on the xy-plane.
Notes:
Example
- 1.
- Calculate the flux of the vector field
 through the upper hemisphere of x2+y2+z2=4 that lies above the rectangle
through the upper hemisphere of x2+y2+z2=4 that lies above the rectangle 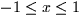 ,
, 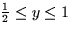 , oriented upward.
Since the surface consists of the upper hemisphere we can solve the equation
of the sphere for
, oriented upward.
Since the surface consists of the upper hemisphere we can solve the equation
of the sphere for 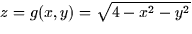 , so the surface is the
graph of a function and we can use
, so the surface is the
graph of a function and we can use 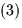 to find
to find 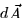 .
.

The flux integral is
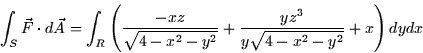
Where R is the rectangle 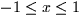 ,
, 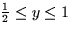 . Now
substitute
. Now
substitute 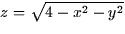 to eliminate the z dependence in the
integral. The integral reduces to
to eliminate the z dependence in the
integral. The integral reduces to
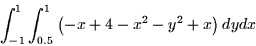
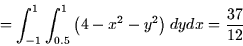



Next: Flux Through Cylinders
Up: The flux Integral
Previous: Introduction
Vector Calculus
8/21/1998
![]() and dS. If the surface S is defined by a
function, z=g(x,y) we can obtain a nice expression for
and dS. If the surface S is defined by a
function, z=g(x,y) we can obtain a nice expression for ![]() and dS.
For the normal vector to S at the point (x0,y0,g(x0,y0)) we
can use the normal vector to the tangent plane. Remember that the tangent
plane to g(x,y) at the point (x0,y0) is given by:
and dS.
For the normal vector to S at the point (x0,y0,g(x0,y0)) we
can use the normal vector to the tangent plane. Remember that the tangent
plane to g(x,y) at the point (x0,y0) is given by:
![]()
![]()
![]()
![]()
![]() ,
, ![]() which define the edges of the patch (one parallel to the xz-plane and one parallel to the yz-plane????). The area of the patch is
given by
which define the edges of the patch (one parallel to the xz-plane and one parallel to the yz-plane????). The area of the patch is
given by ![]() . If we employ the tangent
plane approximation of g(x,y)we can see that
. If we employ the tangent
plane approximation of g(x,y)we can see that ![]() is the vector from (x0,y0,g(x0,y0)) to
is the vector from (x0,y0,g(x0,y0)) to ![]() or
or
![]()
![]()
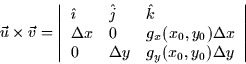
![]()
![]()
![]()
![]()
![]()
![]()
![]()

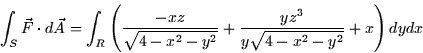
![]()
![]()