


Next: Flux Through Spheres
Up: Flux Integrals
Previous: Flux through Surfaces defined
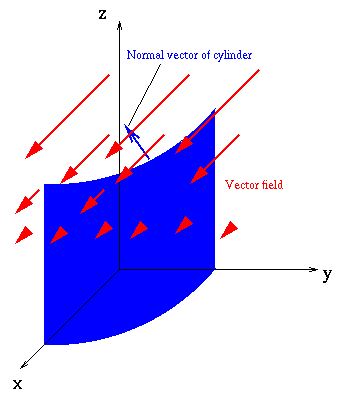
Suppose we want to compute the flux through a cylinder of radius R,
whose axis is aligned with the z-axis. An element of surface area for
the cylinder is
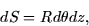
as seen from the picture below.
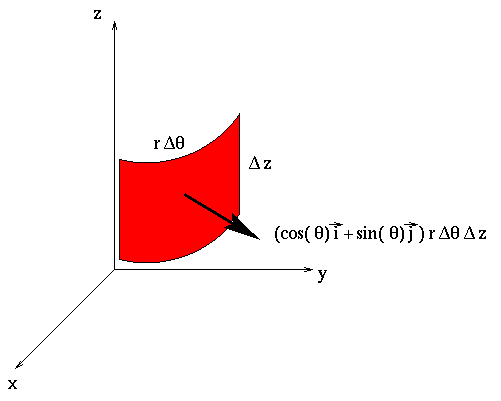
What is the outward normal vector for this surface? It should point in the
straight out from the z-axis, so it should be a unit vector in the
direction of 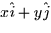 . Thus,
. Thus,
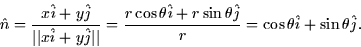
This gives us the result that the flux through a portion of the surface of
a cylinder of radius R oriented along the z-axis is
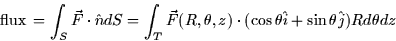
where T is the 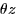 -region corresponding to S.
-region corresponding to S.
Here's a quick example: Compute the flux of the vector field
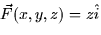 through the piece of the cylinder of radius 3,
centered on the z-axis, with
through the piece of the cylinder of radius 3,
centered on the z-axis, with 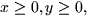 and
and 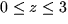 .The cylinder is oriented along the z-axis
and has an inward pointing normal vector.
.The cylinder is oriented along the z-axis
and has an inward pointing normal vector.
- 1.
- Clearly, the flux is negative since the vector field points away from
the z-axis and the surface is oriented towards the z-axis.
- 2.
- The area element is
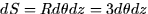 .
. - 3.
- The unit outward normal is
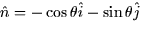 .
. - 4.
- The vector field, in cylindrical coordinates, is
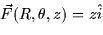 .
. - 5.
- The region T is defined by
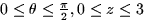 .
. - 6.
- The flux is

![\begin{displaymath}
= -\int^3_0 \int^{\pi/2}_0 3z \cos \theta d\theta dz = -3 \int_0^3 z
[\sin \theta ]_0^{\pi/2} dz
\end{displaymath}](img99.gif)
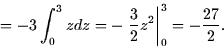



Next: Flux Through Spheres
Up: Flux Integrals
Previous: Flux through Surfaces defined
Vector Calculus
8/21/1998
![]()

![]() . Thus,
. Thus,
![]()
![]()
![]() through the piece of the cylinder of radius 3,
centered on the z-axis, with
through the piece of the cylinder of radius 3,
centered on the z-axis, with ![]() and
and ![]() .The cylinder is oriented along the z-axis
and has an inward pointing normal vector.
.The cylinder is oriented along the z-axis
and has an inward pointing normal vector.

![]()
![]()
![]()