More on breaking up a region

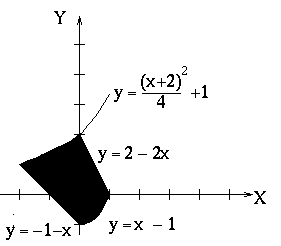
Here's a region that will test your ability to set up an iterated integral. Let's try to set up the iterated integral with both orders of integration for some function f over the region R shown here.

1.

Left to right, then bottom to top To do this, we will need three integrals, since the boundaries are not smooth We need to break R up into the regions R₁, R₂, R₃ shown here:

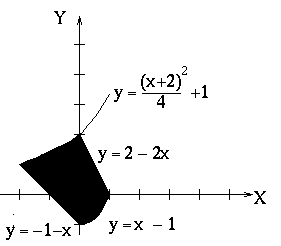
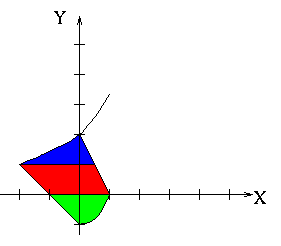
Here are the boundaries for each of the three regions (the left and right boundary functions are gotten from inverting the equations for the appropriate side of the region to get x as a function of y):

 

$$x = 2\sqrt{y - 1} - 2$$ left

right x = 1 - y/2

bottom y = 1

top y = 2

 

left x = -1 - y

right x = 1 - y/2

bottom y = 0

top y = 1

 

left x = -1 - y

$$x = \sqrt{y + 1}$$ right

bottom y = -1

top y = 0

The integral is then

$$\int_R fdA = \int_{R_1} fdA + \int_{R_2}fdA + \int_{R_3}fdA$$

$$= \int_1^2 \int_{2\sqrt{y - 1}-2}^{1-\frac{1}{2}y} f(x,y) dx dy + \int_0^1 \int_{-1-y}^{1 - \frac{1}{2}y} f(x,y) dx dy$$

$$+ \int_{-1}^0 \int_{-1 - y}^{\sqrt{y+1}} f(x,y) dx dy.$$

2.

Bottom to top, then left to right

Here, we'll only need two integrals, as we can break R into the regions R₁ and R₂ as shown:

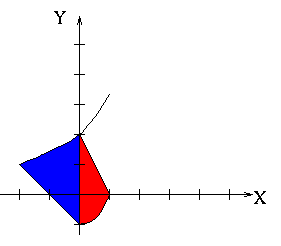
Now we write down the equations for each of the boundaries:

 

left x = -2

right x = 0

bottom y = -x - 1

$$y = \frac{1}{4}(x+2)^2 + 1$$ top

 

left x = 0

right x = 1

bottom y = x² - 1

top y = 2 - 2x

The integral is then

$$\int_R fdA = \int_{R_1} fdA + \int_{R_2}fdA$$

$$= \int_{-2}^0 \int_{-x-1}^{\frac{1}{4}(x+2)^2+1}f(x,y)dy dx + \int_0^1 \int_{x^2 - 1}^{2 -2x} f(x,y) dy dx.$$

Depending on what f is, the second integral is probably easier, since we only needed to break the region into two pieces. Be careful, though. Just because the drawing of the region had the boundaries given as y = y(x) does not mean that it's easier to integrate y first then x. Imagine if we rotated the region R ninety degrees. Then the number of integrals to do each order would swap, but we'd still specify the boundaries as y = y(x) since we're more used to that.